A continuación, presentamos la solución a una serie de ejercicios de programación lineal. Encontrarán diversas variaciones del problema básico, aplicadas en diversos contextos. Los invitamos también a repasar los conceptos relacionados con:
Problema No. 1
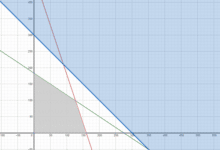
Un herrero con 80 Kg. de acero y 120 Kg. de aluminio quiere hacer bicicletas de paseo y de montaña que quiere vender, respectivamente a 20.000 y 15.000 pesos cada una para sacar el máximo beneficio. Para la de paseo empleará 1 Kg. De acero y 3 Kg. de aluminio, y para la de montaña 2 Kg. de ambos metales. ¿Cuántas bicicletas de paseo y de montaña deberá fabricar para maximizar las utilidades?

Definición de variables
X = Cantidad de bicicletas de paseo a producir.
Y = Cantidad de bicicletas de montaña a producir.
Restricciones
X + 2Y <= 80 (Disponibilidad de acero)
3X + 2Y <= 120 (Disponibilidad de aluminio)
X; Y >= 0 (Restricciones de NO negatividad)
Función objetivo
Zmax = 20000X + 15000Y
Solución del modelo mediante SOLVER

Problema No. 2
Un autobús que hace el recorrido Cali-Buga, ofrece asientos para fumadores al precio de 10.000 pesos y a no fumadores al precio de 6.000 pesos. Al no fumador se le deja llevar 50 Kg. de peso y al fumador 20 Kg. Si el autobús tiene 90 asientos y admite un equipaje de hasta 3.000 Kg. ¿Cuál ha de ser la oferta de asientos de la compañía para cada tipo de pasajeros, con la finalidad de optimizar el beneficio? Además, debe considerarse que por políticas de la empresa, deben ofrecerse cómo mínimo 10 asientos para pasajeros no fumadores.

Definición de variables
X = Cantidad de asientos reservados a fumadores.
Y = Cantidad de asientos reservados a no fumadores.
Restricciones
20X + 50Y <= 3000 (Equipaje permitido)
X + Y <= 90 (Asientos disponibles)
Y >= 10 (Políticas no fumadores)
X; Y >= 0 (No negatividad)
Función objetivo
Zmax = 10000X + 6000Y
Solución mediante SOLVER

Problema No. 3
Un comerciante acude al mercado popular a comprar naranjas con 50.000 pesos. Le ofrecen dos tipos de naranjas: las de tipo A a 50 pesos el Kg. y las de tipo B a 80 pesos el Kg. Sabiendo que sólo dispone de su camioneta con espacio para transportar 700 Kg. de naranjas como máximo y que piensa vender el Kg. de naranjas tipo A a 58 pesos. y el Kg. de tipo B a 90 pesos. plantee un modelo de programación lineal que permita resolver la situación anterior.

Definición de las variables
X = Cantidad de Kg de naranjas tipo A a comprar.
Y = Cantidad de Kg de naranjas tipo B a comprar.
Restricciones
50X + 80Y <= 50.000 (Dinero disponible para comprar)
X + Y <= 700 (Capacidad de transporte)
Función Objetivo
Zmax = 8X + 10Y
Solución obtenida mediante SOLVER

Problema No. 4
Un vendedor de frutas necesita 16 cajas de naranjas, 5 de plátanos y 20 de manzanas. Dos mayoristas están en condiciones de satisfacer sus necesidades, pero solo venden la fruta en contenedores completos. El mayorista A envía en cada contenedor 8 cajas de naranjas, 1 de plátanos y 2 de manzanas. El mayorista B envía en cada contenedor 2 cajas de naranjas, una de plátanos y 7 de manzanas. Sabiendo que el mayorista A se encuentra a 150 Km. de distancia y el mayorista B a 300 Km., calcular cuántos contenedores habrá de comprar a cada mayorista, con el objeto de ahorrar tiempo y dinero, reduciendo al mínimo la distancia.

Definición de variables
X = Cantidad de contenedores a comprar del mayorista A.
Y = Cantidad de contenedores a comprar del mayorista B.
Restricciones
8X + 2Y >= 16 (Requerimiento mínimo de naranjas)
X + Y >= 5 (Requerimiento mínimo de plátanos)
2X + 7Y >= 20 (Requerimiento mínimo de manzanas)
Función Objetivo (Minimizar distancia)
Zmin = 150X + 300Y
Solución obtenida mediante SOLVER

Problema No. 5
Un proveedor debe preparar con 5 bebidas de fruta en existencia, al menos 500 galones de un ponche que contenga por lo menos 20% de jugo de naranja, 10% de jugo de toronja y 5% de jugo de arándano. Si los datos del inventario son los que se muestran en la tabla siguiente ¿Qué cantidad de cada bebida deberá emplear el proveedor a fin de obtener la composición requerida a un costo total mínimo?

Definición de variables
A = Cantidad de galones de la bebida A a utilizar en el ponche.
B = Cantidad de galones de la bebida B a utilizar en el ponche.
C = Cantidad de galones de la bebida C a utilizar en el ponche.
D = Cantidad de galones de la bebida D a utilizar en el ponche.
E = Cantidad de galones de la bebida E a utilizar en el ponche.
Restricciones
A + B + C + D + E >= 500 (Requerimientos de Ponche)
A <= 200 (Disponibilidad de bebida A)
B <= 400 (Disponibilidad de bebida B)
C <= 100 (Disponibilidad de bebida C)
D <= 50 (Disponibilidad de bebida D)
E <= 800 (Disponibilidad de bebida E)
0,4A + 0,05B + C >= 0,2(A + B + C + D + E) Contenido de jugo de naranja
0,4A + 0,1B + D >= 0,1(A + B + C + D + E) Contenido de jugo de toronja
0,2B >= 0,05(A + B + C + D + E) Contenido de jugo de arándano
Función Objetivo
Zmin = 1,5A + 0,75B + 2,00C + 1,75D + 0,25E
Solución obtenida mediante Solver





Buenas, me podrían ayudar con este problema, ya tengo las restricciones pero no puedo determinar su función objetivo, o no lo estoy pillando o se omitió algunos datos, aguardo su ayuda muchas gracias
Un médico le ha diagnosticado a un paciente una falta de vitaminas, para lo
cual diariamente ha de tomar como mínimo 45 unidades de vitamina A, 34 de la vitamina B y 20
de la vitamina C. En la farmacia dispone de los productos X e Y, compuesto cada uno de las
unidades dadas en la tabla siguiente. Se pide minimizar el número de pastillas a consumir.
Producto Vitamina A Vitamina B Vitamina C
X 5 3 1
Y 3 2 4
Determine
1. La ecuación que se trata de minimizar o maximizar.
2. El planteamiento algebraico de las restricciones.
3. Representa la región factible.
4. La combinación óptima de los dos productos X e Y.
5. La utilidad máxima o mínima posible, utilizando la combinación óptima de los
productos.
Buenas cesar la solucion es la siguiente:
se debe minimizar el numero de pastillas a consumir, por lo tanto queda minimizar z = x + y
va a estar sujeto a : 5x+3y≥45, 3x+2y≥35 y 1x+4y≥20
queria saber como plantear una ecuacion de restriccion ,segun este texto, la proporcion del dinero invertido , debe ser a los sumo
de 4/5.
x1<=(4/5)x1
X1 es el dinero invertido, la restriccion indica que la proporcion del dinero invertido debe ser entre 0 y 4/5 de esa cantidad
Hola me podrian ayudar con este problema, no estoy muy segura de la funsion onjetivo. =).
brica mexicana de juguetes Matel, está en el proceso de evaluar, la factibilidad de fabricar tres nuevos juguetes (1, 2 y 3) para la próxima navidad. Dado la incertidunbre económica provocado por la pandemia SARS-COV-2. Para poder realizar el proyecto es necesario reacondicionar las instalaciones para la fabricación de estos tres nuevos modelos, con los siguientes costos para el modelo 1, el costo de reacodicionamiento sería de $25,000; para el modelo 2, el costo de reacondicionamiento sería de $35,000; y finalmente para el modelo 3, el costo sería $30,000. La ganancia por cada juguete son los siguientes, por el modelo 1 es $ 200.00; por el modelo 2 $ 300.00 y por el modelo 3 $360.00. Matel cuenta con tres plantas en México, una Sonora, una en la Ciudad de México y otra en Puebla, que pueden producir los nuevos modelos de juguetes, dependiendo cual de ellas garantice la máxima ganancia. Por lo tanto para evitar costos innecesarios, solo una de ellas se encargará de la fabricación de estos tres nuevos modelos.
Consideraciones:
El número de horas que requiere cada planta para producir cada juguete se muestra en la siguiente matriz
NUEVOS JUGUETES
PLANTA MODELO 1 MODELO 2 MODELO 3
sonora 5 4 6
ciudad de mexico 4 2 2
puebla 3 3 2
Disponibilidad de horas de producción
PLANTA Horas disponibles de producción al día
sonora 500
ciudad de mexico 600
puebla 630
gracias.
Hola me puede ayudar con este ejercicio
Una librería requiere establecer la demanda de una novela para los próximos 4 meses. Actualmente, dispone de 110 unidades en inventario. La proyección de la demanda es la siguiente:
Mes 1 130 unidades
Mes 2 290 unidades
Mes 3. 190 unidades
Mes 4. 150 unidades
La librería tiene la capacidad de adquirir hasta 300 libros cada mes, a un costo de $ 4.000 por libro.
Los libros producidos adquiridos en un mes pueden ser vendidos en ese período o quedar almacenados para otro mes. Cada unidad almacenada tiene un costo adicional de $ 300 por mes.
Se debe determinar el modelo final que permita satisfacer la demanda y a un costo mínimo.
Definir el problema
Determinar la función objetivo y las restricciones
Expresar el modelo final
Este ejercicio está desarrollado en: https://ingenieriaindustrialonline.com/investigacion-de-operaciones/ejercicios-de-programacion-lineal-4
1. Cierta empresa produce dos tipos de bicicletas, la deportiva y la de montaña. Ambos tipos
de bicicleta se producen en dos departamentos de producción, de acuerdo a los siguientes
requerimientos semanales de mano de obra:
TIPO DE
BICICLETA
REQUERIMIENTOS DE
PRODUCCIÓN
UTILIDAD
UNITARIA
DEPTO. 1 (hrs.) DEPTO. 2 (hrs.)
DEPORTIVA 2 3 $ 1,500
DE MONTAÑA 3 4 $ 1,800
M. DE O. DISP.
POR SEMANA 100 100
Los administradores de la empresa se han fijado las siguientes metas, en orden de
importancia:
P1 : No subutilizar la mano de obra disponible.
P2 : Cubrir una demanda de 10 bicicletas de cada tipo por semana.
P3 : Lograr una utilidad semanal mínima de $ 50,000.
Plantee y resuelva este problema utilizando la programación por metas para ayudar a los
administradores de la empresa a lograr sus objetivos.
2. Un pequeño fabricante de equipo especial de productos de oficina fabrica dos clases de
productos, sillas y lámparas. El margen bruto de la venta de una silla es $80; el de la venta
de una lámpara, $40. La producción de una silla requiere 2 horas, mientras que la de una
lámpara requiere de 4 horas, y la capacidad del departamento de producción es de 40
horas por semana. Debido a la capacidad limitada en las ventas, el máximo número de
sillas y lámparas que puede venderse es de 6 y 8 por semana respectivamente. Las metas
que se ha fijado el gerente son, en orden de importancia:
P1 : Lograr una utilidad bruta de $640 la semana siguiente.
P2 : Evitar la subutilización de la capacidad de producción.
P3 : Vender tantas sillas y lámparas como sea posible.
P4 : Minimizar el tiempo extra de la planta tanto como sea posible.
Formule este problema como un problema de programación meta, para que el gerente de la
empresa pueda tomar una decisión que cumpla sus metas tanto como se pueda.
3. Una empresa manufacturera produce congeladores. La compañía tiene dos líneas de
producción. La tasa de producción para la línea 1 es 3 unidades por hora y para la línea 2
es de 2 unidades por hora. La capacidad regular de producción es de 40 horas por semana
para ambas líneas. La utilidad bruta de un congelador es de $125. El presidente de la
compañía tiene las siguientes metas para la semana siguiente, que se muestran en orden
descendente de prioridad.
P1 : Cumplir la meta de producción de 200 unidades por semana.
P2 : Limitar la operación de tiempo extra de la línea 2 a 5 horas.
P3 : Evitar la subutilización de las horas normales de trabajo de ambas líneas.
P4 : Minimizar el tiempo extra para ambos grupos.
Resuelva este problema mediante la programación por metas para que pueda hacer
recomendaciones al gerente, y así ayudarlo a lograr sus metas.
me podrían ayudar con este problema
El entrenador Flakey Waters del equipo de futbol de la Oconee High School tiene disponibles tres jugadores que puede utilizar en forma indistinta en la defensa. Cualquiera delos tres jugadores puede jugar en cualquiera de las tres posiciones de quarterback, fullback o tail back. Para el juego del campeonato estatal que está por llevarse acabo, el entrenador desea maximizar la cantidad combinada de avance que se logra con los tres jugadores colocándolos en la mejor posición. Ha revisado su desempeño anterior en cualquiera de esas posiciones y ha calculado las yardas promedio que han ganado por juego.
Hola ¿tendras la respuesta?
hola me pdrian ayudar con este ejercicio por favor
Una empresa produce gaseosas en tres sabores: limón, naranja y piña, en sus cuatro plantas: A, B, C y D. La planta A produce al día máximo 1 000 gaseosas de limón, mínimo 3 000 de naranja y máximo 5 000 de piña. La planta B produce diariamente máximo 2 000 gaseosas de cada uno de los sabores.
La planta C produce al día mínimo 3X00 gaseosas de limón, máximo 1y00 de naranja y mínimo 2y00 de piña. La planta D produce diariamente mínimo y000 gaseosas de cada uno de los sabores
La empresa se ha comprometido a entregar a sus clientes máximo y0 000 gaseosas de limón, y60 000 de naranjas y 2X0 000 de piña. Si la ganancia es de S/ y por cada gaseosa que se produce en A, 20% adicional por cada gaseosa que se produce en B con respecto a la gaseosa que se produce en A, 25% menos de la ganancia por cada gaseosa que se produce en C con respecto a la gaseosa que se produce en A, y s/2.5 por cada gaseosa que se produce en D.
Un laboratorio de productos veterinarios distribuye un producto en tres formas de cajas distintas A, B y C. Las cajas del tipo A tienen un peso de 250 gramos y un precio de 600 pesos, las de tipo B pesan 500 gramos y su precio es 1080 pesos mientras que las C pesan 1 kilo y cuestan 1980 pesos. A una veterinaria le suministran un lote de 5 cajas con un peso de 2,5 kilos por un importe de 5.340 pesos. ¿Cuántas cajas de cada tipo se enviaron a la veterinaria?
Este ejercicio está desarrollado en: https://ingenieriaindustrialonline.com/investigacion-de-operaciones/ejercicios-de-programacion-lineal-4
Hola, me podrian ayudar con este ejercicio, por favor.
Una empresa elabora 2 productos A y B, que proporcionan $800 y $1100. Los dos deben pasar por 3 procesos. El articulo A tarde 10 min en proceso de corte, 15min en costura y 12 en detallado, el B tarda 12, 18 y 1o respectivamente. Se dispone de tiempo de corte al dia de 59 hrs, 70 hrs de costura y 65 de detallado, Se debe cumplir tambien una orden especial de un cliente de 30 y 35 respectivamente. ¿Cuántos debe producir al dia ?
Gracias
Este ejercicio está desarrollado en: https://ingenieriaindustrialonline.com/investigacion-de-operaciones/ejercicios-de-programacion-lineal-4
Una compañía fabrica dos productos. Uno y otro deben ser procesados
en dos departamentos. El producto A requiere 2 horas por unidad en el
departamento 1 y 4 horas por unidad en el departamento 2. El producto B
requiere 3 horas por unidad en el departamento 1 y 2 horas por unidad en el
departamento 2. Los departamentos 1 y 2 tienen, respectivamente, 60 y 80
horas disponibles a la semana. Los márgenes de utilidad de los dos productos
son, respectivamente, $3 y $4 por unidad. Si x1 y x2 es el número de
unidades fabricadas del producto A y B respectivamente.
a) Formule el modelo de programación lineal para determinar la mezcla de
productos que maximice las utilidades totales.
b) suponga que un requerimiento adicional es
que el número de unidades fabricadas del producto B debe ser por lo menos el
mismo que el número de unidades fabricadas del producto A. ¿Cuál es la
restricción matemática que representa esta condición?
Yo también tengo duda con este, en espacial la ultima restricción que piden.
Hola me pueden ayudar con este problema?
1.- Un fabricante que produce un solo producto tiene dos tipos de clientes. Si se producen unidades para el cliente 1, entonces el cliente 1 estará dispuesto a pagar un precio de UM. Si se producen unidades para el cliente 2, entonces el cliente 2 estará dispuesto a pagar un pre¬cio de UM. El costo de producción es 100 + 15(q1+q2) UM, donde 100 UM es el costo fijo y se paga una sola vez. ¿Cuántas unidades debería vender a cada cliente para maximizar su ganancia?
Determine las cantidades a vender y la ganancia máxima, justifique
Una empresa restaurantera ofrece 4 paquetes de desayunos que contienen lo siguiente:
A B C D
Bebida 2 1 1 1 180
Almuerzo 1 1 1 1 80
Entrada 1 0 1 1 28
Salsas 3 1 0 1 60
Postre 2 0 0 1 30
Precio de venta $800 $600 $300 $500
*Se sabe que los valores mínimos que el propietario desea vender son:
Paquete A → 20
Paquete B → 2
Paquete C → 0
Paquete D → 8
Hola ¿por casualidad sabes cuál es a fuente original del ejercicio n°5?.
Hola, me gustaría si es posible que alguien me ayude con este problema por favor.
En una huerta se tienen los siguientes cultivos y tiempo de cosecha:
Lechuga: 4 semanas / Tomate: 11 semanas / Rúcula: 4 semanas / Perejil: 5 semanas
Además, los cultivos tienen el ste rendimiento:
Lechuga: 400gr
Tomate: 1000gr
Rúcula: 250gr
Perejil: 250gr
La huerta tienen en total 40 posiciones para poder sembrar y cultivar. A su vez, cada cultivo ocupa una cantidad de espacio y su máximo se encuentra limitado a un Factor de Ocupación por espacio (FO): Lechuga FO=3 / Tomate (FO)=3 / Rúcula (FO)=1 / Perejil (FO)=1. Si se supone que al menos se requiere consumir una unidad de cada cultivo por semana, determinar las cantidades de cultivo máximo por semana para maximizar la rotación de los mismos.
hola me podrian ayudar con este:
Una planta productora de fibras tiene una línea donde produce poliéster, elastano y dacron.
El departamento de hilandería requiere de 20, 40 y 30 horas respectivamente para producir
una tonelada de cada una de las fibras; este departamento cuenta con 2 000 horas. El
departamento de tenido cuenta con 4 800 horas y requiere 70, 80 y 90 horas
respectivamente para teñir una tonelada de fibra. Por último los productos deben ser
colocados en bobinas de 1 kg para su venta. El tiempo requerido es de 25 horas por cada
tonelada de poliéster o de dacron y de 35 horas para bobinar una tonelada de elastano
pues debe realizarse mucho más lentamente para no perder sus propiedades. Se cuenta
con 1 500 horas de bobinadora. Las ventas limitan la producción de dacron a 25 000 kg por
mes. Si los costos de materia prima para las 3 fibras son similares y si el precio de venta es
de 1 000, 1 500 y 2 000 pesos por tonelada, plantéelo como un problema de pl.
Un transportista lleva cítricos de Florida a Montreal. Cada caja de naranjas tiene 4 pies3 de volumen y pesa 80 lb.
Cada caja de toronjas tiene un volumen de 6 pies3 y pesa 100 lb. Su camión tiene una capacidad máxima de 300
pies3 y no puede llevar más de 5600 lb. Además, no se le permite llevar más cajas de toronjas que cajas de naranjas.
Si su utilidad es $2.50 por cada caja de naranjas y $4 por cada caja de toronjas, ¿cuántas cajas de cada cítrico debe
transportar para obtener máxima utilidad?