Programación lineal
La Programación Lineal (Optimización lineal), es el nombre que se le da al cálculo de la mejor solución, a un problema modelado como un conjunto de relaciones lineales. Estos problemas surgen en muchas disciplinas de la ciencia y la ingeniería.
Es comúnmente utilizada en el ejercicio de la ingeniería, para abordar problemas de productividad, de acuerdo a la satisfacción de determinadas restricciones – por ejemplo: recursos, principalmente los limitados y costosos -, de acuerdo a un criterio de optimización: maximizar un beneficio o minimizar un costo.
El objetivo primordial de la Programación Lineal es optimizar, es decir, maximizar o minimizar funciones lineales, en varias variables lineales, con restricciones lineales (sistemas de inecuaciones lineales), optimizando una función objetivo también lineal.
Los resultados y el proceso de optimización se convierten en una base cuantitativa del proceso de toma de decisiones frente a las situaciones planteadas. Decisiones en las que sería importante tener en cuenta diversos criterios adicionales, como:
- Los hechos
- La experiencia
- La intuición
- La autoridad
Es preciso considerar que la solución de un modelo matemático establece una base para la toma de decisiones; sin embargo, puede considerarse como esencial el análisis de los resultados obtenidos.
¿Cómo resolver un problema mediante programación lineal?
El primer paso para la resolución de un problema de programación lineal consiste en la identificación de los elementos básicos de un modelo matemático, estos son:
- Función Objetivo
- Variables
- Restricciones
El siguiente paso consiste en la determinación de los mismos, para lo cual proponemos seguir la siguiente metodología:

La función objetivo
La función objetivo tiene una estrecha relación con la pregunta general que se desea responder. Si en un modelo resultasen distintas preguntas, la función objetivo se relacionaría con la pregunta del nivel superior, es decir, la pregunta fundamental. Así por ejemplo, si en una situación se desean minimizar los costos, es muy probable que la pregunta de mayor nivel sea la que se relacione con aumentar la utilidad en lugar de un interrogante que busque hallar la manera de disminuir los costos.

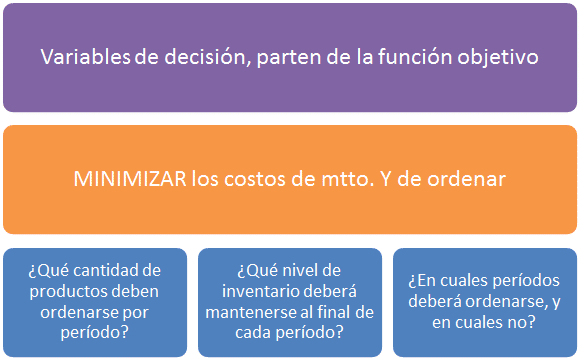
Las variables de decisión
Similar a la relación que existe entre objetivos específicos y objetivo general, se comportan las variables de decisión respecto a la función objetivo, puesto que estas se identifican partiendo de una serie de preguntas derivadas de la pregunta fundamental. Las variables de decisión, son en teoría, factores controlables del sistema que se está modelando, y como tal, estas pueden tomar diversos valores posibles, de los cuales se precisa conocer su valor óptimo, que contribuya con la consecución del objetivo de la función general del problema.
Las restricciones
Cuando hablamos de las restricciones en un problema de programación lineal, nos referimos a todo aquello que limita la libertad de los valores que pueden tomar las variables de decisión.
La mejor manera de hallarlas consiste en pensar en un caso hipotético en el que decidiéramos darle un valor infinito a nuestras variables de decisión, por ejemplo, ¿qué pasaría si en un problema que precisa maximizar sus utilidades en un sistema de producción de calzado decidiéramos producir una cantidad infinita de zapatos? Seguramente ahora nos surgirían múltiples interrogantes, como por ejemplo:
- ¿Con cuánta materia prima cuento para producirlos?
- ¿Con cuánta mano de obra cuento para fabricarlos?
- ¿Pueden las instalaciones de mi empresa albergar tal cantidad de producto?
- ¿Podría mi fuerza de mercadeo vender todos los zapatos?
- ¿Puedo financiar tal empresa?
Pues bueno, entonces habríamos descubierto que nuestro sistema presenta una serie de limitantes, tanto físicas, como de contexto, de tal manera que los valores que en un momento dado podrían tomar nuestras variables de decisión se encuentran condicionados por una serie de restricciones.
Ejemplo de resolución de un problema de programación lineal
El problema se recomienda leer en más de una ocasión para facilitar el reconocimiento de las variables, además es muy recomendable la elaboración de tablas o matrices que faciliten una mayor comprensión del mismo.La fábrica de Hilados y Tejidos «SALAZAR» requiere fabricar dos tejidos de calidad diferente T y T’; se dispone de 500 Kg de hilo a, 300 Kg de hilo b y 108 Kg de hilo c. Para obtener un metro de T diariamente se necesitan 125 gr de a, 150 gr de b y 72 gr de c; para producir un metro de T’ por día se necesitan 200 gr de a, 100 gr de b y 27 gr de c. El T se vende a $4000 el metro y el T’ se vende a $5000 el metro. Si se debe obtener el máximo beneficio, ¿cuántos metros de T y T’ se deben fabricar?
Paso 1: Formular el problema
Para realizar este paso partimos de la pregunta central del problema.
¿Cuántos metros de T y T’ se deben fabricar?
Y la formulación es:
“Determinar la cantidad de metros diarios de tejido tipo T y T’ a fabricar teniendo en cuenta el óptimo beneficio respecto a la utilidad”.
Paso 2: Determinar las variables de decisión
Basándonos en la formulación del problema nuestras variables de decisión son:
XT: Cantidad de metros diarios de tejido tipo T a fabricar
XT’: Cantidad de metros diarios de tejido tipo T’ a fabricar
PASO 3: Determinar las restricciones del problema
En este paso determinamos las funciones que limitan el problema, estas están dadas por capacidad, disponibilidad, proporción, no negatividad entre otras.
De disponibilidad de materia prima:
0,125XT + 0,200XT’ <= 500 Hilo “a”
0,150XT + 0,100XT’ <= 300 Hilo “b”
0,072XT + 0,027XT’ <= 108 Hilo “c”
De no negatividad
XT,XT’ >= 0
PASO 4: Determinar la Función Objetivo
En este paso es de vital importancia establecer el contexto operativo del problema para de esta forma determinar si es de Maximización o Minimización. En este caso abordamos el contexto de beneficio por ende lo ideal es Maximizar.
Función Objetivo
ZMAX = 4000XT + 5000XT’
PASO 5: Resolver el modelo utilizando software o métodos manuales
La solución de un modelo de programación lineal puede abordarse de diversas formas: métodos manuales (Simplex), métodos gráficos y solucionadores (software).
La consideración del método manual Simplex, y el método gráfico tiene un fundamento pedagógico. La perspectiva de lo que representa un modelo de programación lineal, se amplía considerablemente mediante estos métodos.
Ahora bien, en la práctica, los métodos utilizados por excelencia son los solucionadores (software). Programas de computación que utilizan algoritmos que permiten resolver modelos robustos con suma facilidad. Dentro de los solucionadores más tradicionales encontramos:
Son programas gratuitos, a menudo restringidos en cuanto al número de variables y restricciones, y por estos días, muchos de ellos descontinuados.
En la actualidad, los solucionadores de programación basada en restricciones, ofrecen la mejor de las prestaciones. Son robustos, se encuentran integrados y algunos de ellos son gratuitos, como es el caso de Google OR-Tools.
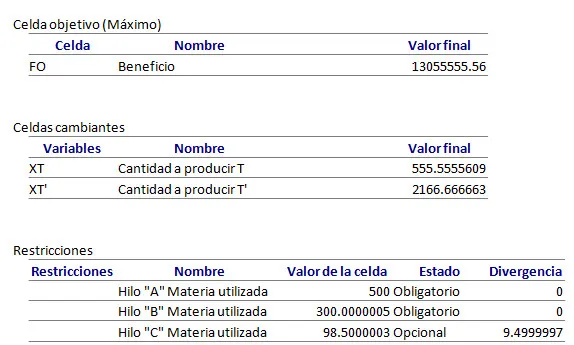
Para efectos prácticos, el anterior ejercicio fue resuelto mediante Solver – Excel, y su resultado fue:
Hemos preparado una serie de ejercicios de programación lineal y programación lineal entera, en los cuales podrá observar su modelamiento y resolución en Solver.




Hola Bryan muy buena pagina y te quería hacer una pregunta me gustaba mas la otra forma de la pagina, pero te quería pedir un favor me podrías mandar el listado de temas para Investigación de Operaciones, ya que en esta forma de la pagina es un poco confusa, muchas gracias.
Si es programacion lineal solamente. 1. Formular el problema planteando las tres partes.a) Funcion objetivob);restricciones estructurales( los recursos).c)condiciones de no negatividad, ya que en investigacion de operaciones todos los productos estan en buena calidad entonces es superior a cero.
Temas de investigacion de operaciones.
1. Problemas de transporte co0n balance y desbalanceado; rutas rpohibidas..
2. Programacion no lineal con ecuaciones de 2do grado. Problema de chalanas.
3. programacion heuristica: sacos para maiz CONASUPO Mexico.
4. Programacion en problemas de rutas: Optimizacion en una gasolinera. y muchos mas escucha mis clases.
Totalment de acuerdo con Douglas.
La version anterior era , desde mi apreciacion , mas entendible.
Saludos cordiales.
Atte.
Luis Olivares
Lima – Peru
Hola Luis… Todos extrañamos esa primera configuración. Sin embargo, los cambios nos han permitido generar nuevas formas de agregar valor. Un saludo, gracias por comentar, y espero que nos visites con frecuencia.
Bryan, muy buena la explicacion
Hola buenas noches, muy interesante me ha sido de mucha ayuda. ¿Donde puedo consultar la bibliografía?