A continuación, presentamos la solución a una serie de ejercicios de programación lineal. Encontrarán diversas variaciones del problema básico, aplicadas en diversos contextos. Los invitamos también a repasar los conceptos relacionados con:
Problema No. 16
Una empresa elabora 2 productos A y B, que proporcionan $800 y $1100. Los dos deben pasar por 3 procesos. El articulo A tarda 10 min en proceso de corte, 15 min en costura y 12 min en detallado. El B tarda 12 min, 18 min y 10 min respectivamente. Se dispone de tiempo de corte al día de 59 h, 70 h de costura y 65 h de detallado. Se debe cumplir también una orden especial de un cliente de 30 y 35 unidades diarias, respectivamente. ¿Cuántos productos de cada tipo debe producir al día?
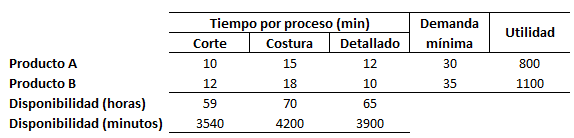
Como Asistente del Departamento de Producción, usted necesita determinar un plan de producción diario óptimo.
Definición de variables
A = Cantidad de unidades de producto «A» a fabricar diariamente
B = Cantidad de unidades de producto «B» a fabricar diariamente
Restricciones
10A + 12B <=3540 (Disponibilidad de minutos de Corte)
15A + 18B <= 4200 (Disponibilidad de minutos de Costura)
12A + 10B <= 3900 (Disponibilidad de minutos de Detallado)
A >= 30 (Demanda mínima «Orden especial»)
B >= 35 (Demanda mínima «Orden especial»)
A; B = Enteros
Función objetivo
Zmax = 800A + 1100B
Solución del modelo mediante SOLVER
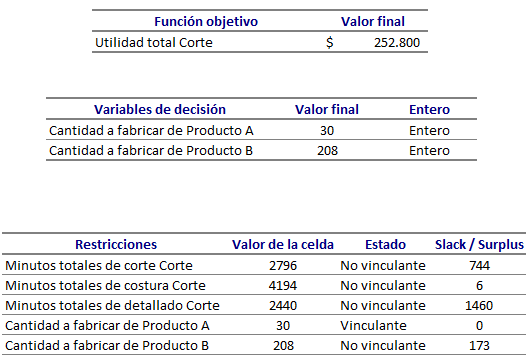
Problema No. 17 (Valor de)
Un laboratorio de productos veterinarios distribuye un producto en tres formas de cajas distintas A, B y C. Las cajas del tipo A tienen un peso de 250 gramos y un precio de 600 pesos, las de tipo B pesan 500 gramos y su precio es 1080 pesos mientras que las C pesan 1 kilo y cuestan 1980 pesos. A una veterinaria le suministran un lote de 5 cajas con un peso de 2,5 kilos por un importe de 5.340 pesos.
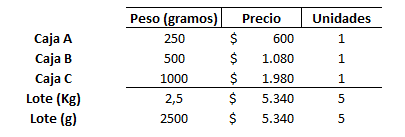
¿Cuántas cajas de cada tipo se enviaron a la veterinaria?
Definición de variables
A = Cantidad de cajas tipo A que se enviaron a la veterinaria en el lote
B = Cantidad de cajas tipo B que se enviaron a la veterinaria en el lote
B = Cantidad de cajas tipo C que se enviaron a la veterinaria en el lote
Restricciones
A + B + C = 5
250A + 500B + 1000C = 2500
600A + 1080B + 1980C = 5340
A;B;C = Enteros
Función objetivo (Valor de)
La función objetivo de este problema no consiste en minimizar ni maximizar una ecuación, sino establecer una igualdad, ya sea en función de la restricción de peso o importe.
5340 = 600A + 1080B + 1980C
Solución mediante SOLVER
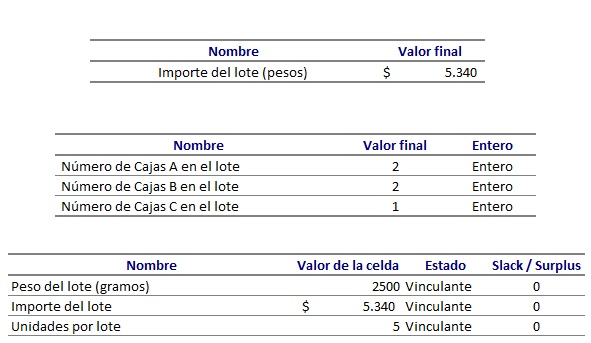
Problema No. 18 (Inventarios)
Una librería requiere establecer la demanda de una novela para los próximos 4 meses. Actualmente, dispone de 110 unidades en inventario. La proyección de la demanda es la siguiente:
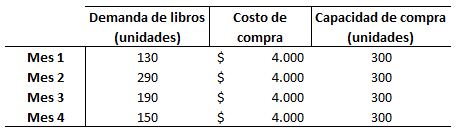
La librería tiene la capacidad de adquirir hasta 300 libros cada mes, a un costo de $4.000 por libro.
Los libros producidos adquiridos en un mes pueden ser vendidos en ese período o quedar almacenados para otro mes. Cada unidad almacenada tiene un costo adicional de $ 300 por mes.
Se debe determinar el modelo final que permita satisfacer la demanda y a un costo mínimo.
Definición de las variables
X1 = Cantidad de libros a comprar en el mes 1.
X2 = Cantidad de libros a comprar en el mes 2.
X3 = Cantidad de libros a comprar en el mes 3.
X4 = Cantidad de libros a comprar en el mes 4.
Ii = Inventario inicial.
I1 = Inventario al final del mes 1.
I2 = Inventario al final del mes 2.
I3 = Inventario al final del mes 3.
Restricciones
Ii = 110 (Inventario inicial)
Restricciones para satisfacer la demanda proyectada
X1 + Ii >= 130 (Compras mes 1 + Inventario inicial >= demanda mes 1)
X2 + I1 >= 290 (Compras mes 2 + Inventario final mes 1 >= demanda mes 2)
X3 + I2 >= 190 (Compras mes 3 + Inventario final mes 2 >= demanda mes 3)
X4 + I3 = 150 (Compras mes 4 + Inventario final mes 3 = demanda mes 4)
Todas las variables = Enteros
Restricciones de balance (Definición de variables de inventarios)
I1 = Ii + X1 – 130 (Inventario final del mes 1 = Inventario inicial + Compras mes 1 – Demanda mes 1)
I2 = I1 + X2 – 290 (Inventario final del mes 2 = Inventario final 1 + Compras mes 2 – Demanda mes 2)
I3 = I2 + X3 – 190 (Inventario final del mes 3 = Inventario final 2 + Compras mes 3 – Demanda mes 3)
Restricciones de capacidad de compra
X1 <= 300
X2 <= 300
X3 <= 300
X4 <= 300
Enteros
X1;X2;X3;X4 = Enteros
Función Objetivo
Zmin = 4000(X1 + X2 + X3 + X4) + 300(I1 + I2 + I3)
Solución obtenida mediante SOLVER
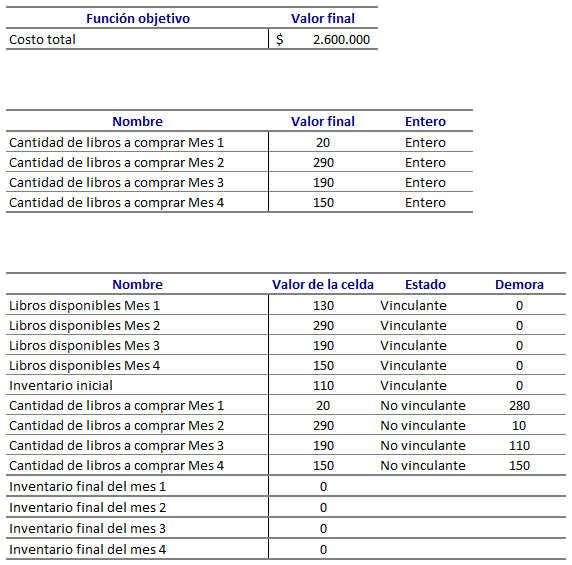
*La respuesta de este ejercicio parece evidente, la formulación tomaría relevancia en la medida en que varíen los precios de adquisición de libros de un mes a otro.
Problema No. 19
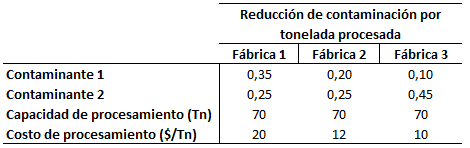
Una empresa posee 3 fábricas instaladas a la orilla de un río; cada una de las fábricas arroja 2 tipos de contaminante al río. Si la basura es procesada en cada fábrica, es posible reducir el contaminante vertido al río. Cuesta 20 dólares procesar una tonelada de basura de la fábrica 1, reduciendo en 0,35 toneladas el contaminante 1 y en 0,25 toneladas el contaminante 2. Cuesta 12 dólares procesar una tonelada de basura de la fábrica 2, reduciendo en 0,2 toneladas el contaminante 1 y en 0,25 toneladas el contaminante 2. Cuesta 10 dólares procesar una tonelada de basura de la fábrica 3, reduciendo en 0,1 toneladas el contaminante 1 y en 0,45 toneladas el contaminante 2.
Por otro lado, la ley obliga a la empresa a reducir la contaminación total vertida al río en al menos 35 toneladas del contaminante 1 y en al menos 40 toneladas del contaminante 2. Cada fábrica tiene la posibilidad de procesar a lo más 70 toneladas de basura.
Formule y resuelva un modelo de programación Lineal para ayudar a la empresa a minimizar el costo de
reducir la contaminación. Defina sus variables de decisión, explique todas las restricciones y supuestos del
modelo.
Definición de variables
A = Cantidad de toneladas procesadas en la fábrica 1
B = Cantidad de toneladas procesadas en la fábrica 2
C = Cantidad de toneladas procesadas en la fábrica 3
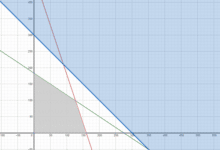
Restricciones
0.35A + 0.20B + 0.10C >= 35 (Reducción mínima contaminante 1)
0.25A + 0.25B + 0.45C >= 40 (Reducción mínima contaminante 2)
12A + 10B <= 3900 (Disponibilidad de minutos de Detallado)
A <= 70 (Capacidad de procesamiento de la fábrica 1)
B <= 70 (Capacidad de procesamiento de la fábrica 2)
C <= 70 (Capacidad de procesamiento de la fábrica 3)
Función objetivo
Zmix = 20A + 12B + 10C
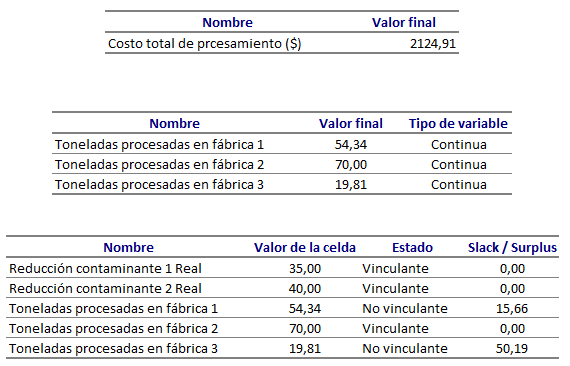
Solución del modelo mediante SOLVER



hola! me podrias ayudar:
Una empresa posee 3 fábricas instaladas a la orilla de un río; cada una de las fábricas arroja 2 tipos de
contaminante al río. Si la basura es procesada en cada fábrica, es posible reducir el contaminante vertido al río.
Cuesta 20 dólares procesar una tonelada de basura de la fábrica 1, reduciendo en 0,35 toneladas el contaminante
1 y en 0,25 toneladas el contaminante 2. Cuesta 12 dólares procesar una tonelada de basura de la fábrica 2,
reduciendo en 0,2 toneladas el contaminante 1 y en 0,25 toneladas el contaminante 2. Cuesta 10 dólares
procesar una tonelada de basura de la fábrica 3, reduciendo en 0,1 toneladas el contaminante 1 y en 0,45
toneladas el contaminante 2. Por otro lado, la ley obliga a la empresa a reducir la contaminación total vertida al
río en al menos 35 toneladas del contaminante 1 y en al menos 40 toneladas del contaminante 2. Cada fábrica
tiene la posibilidad de procesar a lo más 70 toneladas de basura.
a) Formule y resuelva un modelo de programación Lineal para ayudar a la empresa a minimizar el costo de
reducir la contaminación. Defina sus variables de decisión, explique todas las restricciones y supuestos del
modelo.
b) Analice y discuta sus resultados.
c) Comente sobre posibles extensiones para este problema.
Ya ha sido modelado. Un saludo
Ayúdame con este ejercicio
La Mabel’s Toy Shoppe quiere gastar $1 000 en publicidad local. El objetivo global es alcanzar la máxima audiencia posible al mismo tiempo que llegar hasta 6 000 niños por lo menos. Se dispone de tres medios; sus costos y la audiencia que tienen se da en la tabla que sigue:
a) Formúlese éste como un problema de PL y resuélvase. ¿Cuál es la mezcla óptima de publicidad?
b ¿Existe otra mezcla óptima? Si existe, ¿cuál es? ¿Existe alguna razón para preferir alguna?
c ¿En cuánto podría aumentarse la audiencia con $1 adicional en elpresupuesto? ¿Cuál es el rango para el que este valor marginal es válido?
d Una revista local ha ofrecido garantizar una audiencia de 12 000 con 2 000 niños por un costo de $300. ¿Debe considerarse esta oferta?
e Un amigo comentó a Mabel que las abuelas compran muchos juguetes. Ahora quiere estar segura de que la publicidad llega por lo menos a 1 000 abuelas. El periódico, la radio y la televisión dicen que sus anuncios llegan a 200, 100 y 500 por paquete comercial, respectivamente. ¿Cambiará la solución óptima con esta nueva restricción?
f Mabel está preocupada, ya que la audiencia total del periódico sólo es aproximada. ¿Sobre qué rango de audiencia total permanecerá el periódico en la solución?