Programación lineal entera con Google OR-Tools
Básicamente, la diferencia entre programación lineal (PL) y programación lineal entera (PLE) consiste en la naturaleza de sus variables; en el caso de la optimización lineal simple, el uso de variables de naturaleza continua permite el uso de valores fraccionarios en sus variables de decisión; lo cual, de acuerdo al modelo, puede ajustarse a la realidad, o no. Por ejemplo, pensemos en la producción de maíz, es posible procesar fácilmente 1,7 toneladas del grano; en cuyo caso, las variables continuas ajustarán el modelo a la realidad.
Ahora bien, existen innumerables casos de aplicación práctica en los cuales las soluciones fraccionarias no se ajustan a la realidad y debemos considerar el uso de variables enteras, así entonces, tendremos un modelo de programación lineal entera (PLE). Por ejemplo, pensemos en la producción de lápices, es posible que queramos determinar la producción en términos de unidades de producto, no tanto así de fracciones.
Es preciso mencionar que, cuando un modelo presenta todas sus variables enteras, se denomina puro. En caso contrario, cuando utiliza una combinación de variables enteras y continuas, se denomina mixto, y se abordará mediante programación lineal mixta.
Ciertamente, en la práctica, los solucionadores de modelos de optimización han abordado la naturaleza de las variables brindando relativa facilidad; es decir, podemos cambiar el tipo de variable entre continua y entera de una manera muy sencilla, sin que esto afecte considerablemente el modelo.
El objetivo de este artículo consiste en utilizar las librerías del software Google OR-Tools para abordar problemas de programación lineal entera (optimización lineal entera).
OR-Tools proporciona dos herramientas principales para resolver este tipo de problemas de optimización:
- MPSolver: un contenedor para varios solucionadores de MIP de terceros, que utilizan técnicas estándar de ramificación y vinculación (branch and bound).
- Solucionador de CP-SAT: Un solucionador de programación de restricciones que utiliza métodos SAT (satisfacibilidad).
El problema
Con el propósito de evaluar los resultados obtenidos a través del tratamiento de un problema técnicamente formulado y abordado, utilizaremos un caso descrito en el libro Investigación de Operaciones (9na edición), de Hamdy A. Taha (University of Arkansas, Fayetteville), (Conjunto de problemas 9.1A – Problema 3).
Suponga que tiene 7 botellas de vino llenas, 7 a la mitad y 7 vacías. Le gustaría dividir las 21 botellas entre tres individuos de modo que cada uno reciba exactamente 7. Además, cada individuo debe recibir la misma cantidad de vino. Exprese el problema como restricciones del PLE, y halle una solución. TAHA
| Botellas llenas | Botellas a la mitad | Botellas vacías | |
| Contenido | 1 | 0,5 | 0 |
| Cantidad de botellas | 7 | 7 | 7 |
Modelamiento del problema
El problema plantea un caso de asignación, en el cual debemos determinar la cantidad de botellas de cada tipo (llenas, medias y vacías), asignadas a cada uno de un conjunto de 3 individuos (1, 2 y 3). Por lo tanto, las variables de decisión se definirán de la siguiente manera:
xij = Cantidad de botellas de tipo i asignadas al individuo j
i = {0 = Llena; 1 = Media; 2 = Vacía}
j = {0 = Individuo 1; 1 = individuo 2; 2 = individuo 3}
Donde todos los xij son enteros no negativos. (Ya que queremos determinar cantidad de botellas, es decir que las variables de decisión no están formuladas en función del contenido).
Este modelo puede abordar las restricciones de volumen de líquido (contenido igual para todos los individuos), por medio de coeficientes de contenido, o, definiendo que el contenido corresponde a una variable, la cual debe declararse de igual forma. Ya que el contenido que se encuentra en una botella llena, por ejemplo, es el mismo sea asignado a cualquier individuo, la manera más simple de abordarlo es por medio de coeficientes.
En la formulación del modelo de Python lo abordaremos por medio de variables con fines prácticos.
La función objetivo es artificial, dado que el modelo no pretende maximizar o minimizar algún factor. Por lo tanto podemos utilizar cualquier coeficiente, por ejemplo cero.
Zmax = 0x00 + 0x01 + 0x02 + 0x10 + 0x11 + 0x12 + 0x20 + 0x21 + 0x22
Sujeto a las siguientes restricciones:
x00 + x01 + x02 = 7
x10 + x11 + x12 = 7
x20 + x21 + x22 = 7
Las anteriores restricciones limitan la disponibilidad de botellas de cada tipo. Es decir, por ejemplo, la sumatoria de botellas llenas enviadas a los individuos 1, 2 y 3 deberá ser igual a 7; así mismo para el restante tipo de botellas.
x00 + x10 + x20 = 7
x01 + x11 + x21 = 7
x02 + x12 + x22 = 7
Las anteriores restricciones indican que cada individuo deberá recibir exactamente 7 botellas sin importar el tipo de las mismas. Es decir, por ejemplo, la sumatoria de botellas tipo 0, 1 y 2 enviadas al individuo 0, deberá ser igual a 7; así mismo para los individuos restantes.
Respecto a las restricciones de contenido, que limitarán el modelo para que cada individuo reciba la misma cantidad de vino, podemos realizar una operación previa, en la cual determinemos la cantidad total de vino disponible.
Vino disponible = 1( 7 botellas llenas) + 0,5( 7 botellas medias)
Vino disponible = 10,5
Así entonces, para que a cada individuo le corresponda la misma cantidad de vino en la distribución de botellas, deberá dividirse el vino disponible entre el total de individuos.
Vino para cada individuo = (10,5 / 3) = 3,5
Así entonces, las restricciones de equidad en la distribución (contenido) serán las siguientes:
x00 + 0,5x10 = 3,5
x01 + 0,5x11 = 3,5
x02 + 0,5x12 = 3,5
Así entonces, tenemos el problema completamente modelado.
Resolución del modelo mediante Google OR-Tools
De acuerdo a lo mencionado en el artículo de introducción a Google OR-Tools, esta herramienta soporta múltiples lenguajes de programación, en esta ocasión, haremos uso del lenguaje de programación Python.
Paso 1: Importar la librería
El siguiente fragmento de código importa las librerías necesarias:
# Importar la librería de Google OR-Tools
from ortools.linear_solver import pywraplp
Paso 2: Declarar el solucionador
El siguiente fragmento de código declara el solucionador SCIP (Solving Constraint Integer Programs), un solucionador de código abierto disponible (Google OR-Tools posee múltiples solucionadores):
solver = pywraplp.Solver.CreateSolver('SCIP')Paso 3: Crear la data del modelo
El siguiente fragmento de código crea la data del modelo. En este caso, la matriz de contenido de las botellas distribuidas a los 3 individuos (matriz 3 x 3).
# Crear la data del modelo de asignación
contenido = [
[ 1, 1, 1],
[0.5, 0.5, 0.5],
[ 0, 0, 0],
]
num_botellas = len(contenido)
num_individuos = len(contenido[0])Paso 4: Crear las variables del modelo
El siguiente fragmento crea las variables del modelo mediante un bucle (Hace uso número de botellas y el número de individuos), definiendo las variables x [i, j]. Así mismo, se declara el rango de valores que pueden tomar las variables, del mismo modo su naturaleza: variables enteras (solver.IntVar). Esta declaración sustituye las restricciones de no-negatividad (0, solver.infinity()), es decir, mayores a cero.
x = {}
for i in range(num_botellas):
for j in range(num_individuos):
x[i, j] = solver.IntVar(0, solver.infinity(), '')
Paso 5: Definir las restricciones del modelo
El siguiente fragmento de código define las restricciones del modelo mediante bucles:
# Restricciones de disponibilidad de botellas de cada tipo = 7
# Para cada i (tipo de botella), suma sus posibles variaciones de j (individuos)
# Por ejemplo, siendo i = 0, sumará X00 + X01 + X02, esta sumatoria
# deberá ser igual a 7 (botellas disponibles de cada tipo)
for i in range(num_botellas):
solver.Add(solver.Sum([x[i, j] for j in range(num_individuos)]) == 7)
# Restricciones de cantidad de botellas asignadas a cada individuo
# Para cada j (individuo), suma sus posibles variaciones de i (tipos de botella)
# Por ejemplo, siendo j = 0, sumará X00 + X10 + X20, esta sumatoria
# deberá ser igual a 7 (botellas asignadas a un individuo sin importar el tipo)
for j in range(num_individuos):
solver.Add(solver.Sum([x[i, j] for i in range(num_botellas)]) == 7)
# Restricciones de equidad en la distribución (utiliza la matriz de contenido)
# Para cada j (individuo), suma los productos de las posibles
# variaciones de i (tipo de botella) por sus coeficientes de contenido
# Por ejemplo, siendo j = 0 y C[i][j] equivalente al contenido
# de una botella tipo i entregado a un individuo tipo j
# sumará (C00 * X00) + (C10 * X10) + (C20 * X20), los valores de C[i][j]
# los tomará de la matriz de contenido. Esta sumatoria
# deberá ser igual a 3,5 (distribución equitativa por individuo)
for j in range(num_individuos):
solver.Add(solver.Sum([contenido[i][j] * x[i, j] for i in range(num_botellas)]) == 3.5)
Paso 6: Definir la función objetivo del modelo
El siguiente fragmento de código define la función objetivo del modelo. Consideremos que no es importante el criterio de la función, tampoco existe un costo asociado a las variables de decisión. Sin embargo, formularemos una función objetivo basada en bucles (utilizando la matriz de contenido), la cual quizá puede ser de utilidad en modelamientos futuros. Los coeficientes de las variables de decisión se basarán en la matriz de contenido (contenido[i][j]).
# Función objetivo
objective_terms = []
for i in range(num_botellas):
for j in range(num_individuos):
objective_terms.append(contenido[i][j] * x[i, j])
solver.Maximize(solver.Sum(objective_terms))
Paso 7: Invocar el solucionador
El siguiente fragmento de código sirve para invocar el solucionador del modelo:
status = solver.Solve()
Paso 8: Definir las salidas del solucionador
# Configura los parámetros de impresión, las salidas del modelo
botellas_ind0 = 0
botellas_ind1 = 0
botellas_ind2 = 0
if status == pywraplp.Solver.OPTIMAL or status == pywraplp.Solver.FEASIBLE:
print('Puntaje total = ', solver.Objective().Value(), '\n')
for i in range(num_botellas):
for j in range(num_individuos):
# Test if x[i,j] is 1 (con tolerancia de punto flotante)
if x[i, j].solution_value() > 0.5:
print('Botellas del tipo %d asignadas al individuo %d. Cantidad = %d' %
(i, j, x[i, j].solution_value()))
for i in range(num_botellas):
botellas_ind0 = x[i, 0].solution_value() + botellas_ind0
for i in range(num_botellas):
botellas_ind1 = x[i, 1].solution_value() + botellas_ind1
for i in range(num_botellas):
botellas_ind2 = x[i, 2].solution_value() + botellas_ind2
print('Número de botellas asignadas al individuo 0:', botellas_ind0)
print('Número de botellas asignadas al individuo 1:', botellas_ind1)
print('Número de botellas asignadas al individuo 2:', botellas_ind2)
En este caso, configuramos las salidas del solucionador. Nos deberá indicar la cantidad de botellas de cada tipo que deberán ser distribuidas a cada individuo. El valor de la función objetivo (contenido total), nos servirá para verificar la solución (10,5).
Como información adicional, hemos configurado algunas impresiones (arbitrarias) para que nos detalle la cantidad de botellas que le deberán ser asignadas a cada individuo.
Es posible que el desarrollo de los ocho pasos anteriores demande algún grado de complejidad subyacente del uso de un lenguaje de programación; sin embargo, es preciso mencionar que, el modelo anterior queda perfectamente configurado, y puede replicarse con modificaciones menores en múltiples problemas de optimización lineal.
¿Cómo ejecutar el modelo?
Alternativa 1, ejecución en nuestro equipo:
Lo primero que debemos considerar, en el caso de que queramos ejecutar este código en nuestro equipo, es que es preciso contar con la instalación de Python en nuestro equipo de cómputo, así mismo debemos contar con la última versión del comando pip y por supuesto, el software OR-Tools. Una guía detallada de la instalación de estos requerimientos la podrás encontrar en el siguiente enlace:
Instalación de OR-Tools para Python
Ahora, lo recomendable es trabajar con algún editor de código práctico (IDE), por ejemplo: Sublime Text, o Spyder (Una herramienta más completa y por ende más robusta y pesada).
Alternativa 2, ejecución en un entorno virtual (Recomendado):
Podemos utilizar del mismo modo, un entorno virtual. En este caso recomendamos el uso de Colaboratory de Google, un entorno que cuenta con todas las herramientas necesarias para nuestros desarrollos. No tendremos que instalar nada en nuestro equipo, y aprovecharemos la potencia de las máquinas de Google.
El código completo de nuestro desarrollo lo presentamos a continuación. También puedes ver el cuaderno de este módulo en nuestro Colaboratory: Programación Lineal Entera.
# Caso: Investigación de Operaciones (9na edición), de Hamdy A. Taha
# (University of Arkansas, Fayetteville), (Conjunto de problemas 9.1A - Problema 3)
# Modelo: MSc. Ing. Bryan Salazar López
# Importar la librería de Google OR-Tools
from ortools.linear_solver import pywraplp
# Declarar el solucionador que abordará el modelo
solver = pywraplp.Solver.CreateSolver('SCIP')
# Data del modelo
contenido = [
[ 1, 1, 1],
[0.5, 0.5, 0.5],
[ 0, 0, 0],
]
num_botellas = len(contenido)
num_individuos = len(contenido[0])
def main():
# Variables del modelo
x = {}
for i in range(num_botellas):
for j in range(num_individuos):
x[i, j] = solver.IntVar(0, solver.infinity(), '')
# Las sumatoria de botellas de cada tipo es igual a 7
# Cada curso podrá tener un máximo de n estudiantes
for i in range(num_botellas):
solver.Add(solver.Sum([x[i, j] for j in range(num_individuos)]) == 7)
for j in range(num_individuos):
solver.Add(solver.Sum([x[i, j] for i in range(num_botellas)]) == 7)
for j in range(num_individuos):
solver.Add(solver.Sum([contenido[i][j] * x[i, j] for i in range(num_botellas)]) == 3.5)
# Función objetivo con criterio de optimización: minimizar
objective_terms = []
for i in range(num_botellas):
for j in range(num_individuos):
objective_terms.append(contenido[i][j] * x[i, j])
solver.Maximize(solver.Sum(objective_terms))
# Invoca el solucionador
status = solver.Solve()
# Configura los parámetros de impresión, las salidas del modelo
botellas_ind0 = 0
botellas_ind1 = 0
botellas_ind2 = 0
if status == pywraplp.Solver.OPTIMAL or status == pywraplp.Solver.FEASIBLE:
print('Contenido total = ', solver.Objective().Value(), '\n')
for i in range(num_botellas):
for j in range(num_individuos):
# Test if x[i,j] is 1 (con tolerancia de punto flotante)
if x[i, j].solution_value() > 0.5:
print('Botellas del tipo %d asignadas al individuo %d. Cantidad = %d' %
(i, j, x[i, j].solution_value()))
for i in range(num_botellas):
botellas_ind0 = x[i, 0].solution_value() + botellas_ind0
for i in range(num_botellas):
botellas_ind1 = x[i, 1].solution_value() + botellas_ind1
for i in range(num_botellas):
botellas_ind2 = x[i, 2].solution_value() + botellas_ind2
print('Número de botellas asignadas al individuo 0:', botellas_ind0)
print('Número de botellas asignadas al individuo 1:', botellas_ind1)
print('Número de botellas asignadas al individuo 2:', botellas_ind2)
if __name__ == '__main__':
main()Al ejecutar nuestro desarrollo en Colaboratory, tenemos:
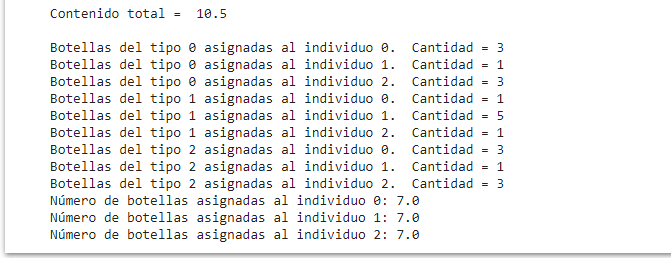
De esta manera se ha hallado una solución óptima al modelo formulado. Esta misma respuesta se encuentra consignada en el libro Investigación de Operaciones de TAHA:
| Individuo 1 | Individuo 2 | Individuo 3 | |
| Botellas llenas | 3 | 1 | 3 |
| Botellas medio llenas | 1 | 5 | 1 |
| Botellas vacías | 3 | 1 | 3 |
Ahora bien, el modelo de optimización lineal y el script del solucionador quedaron desarrollados en un lenguaje de programación estándar y ampliamente utilizado. Desde luego, las posibilidades de integrar datos de entrada y procesar los datos de salidas son interesantes. Por ejemplo, es posible desarrollar un script mediante el cual el código ya desarrollado tome los datos de entrada desde un archivo de Excel, o desde un servidor externo.
También, es posible desarrollar una interfaz amigable desde la cual se ingrese la información; o vincular los datos de salida con algún modelo o documento determinado.
En próximos artículos abordaremos algunos modelos que incorporen la combinación de tipos de variables (continuas y enteras): programación lineal mixta.