Programación lineal en Lingo
LINGO es una herramienta diseñada para construir y resolver modelos de optimización matemática. LINGO proporciona un paquete integrado que incluye un potente lenguaje para expresar modelos de optimización, un ambiente con todas las funciones para los problemas de construcción y edición, y un conjunto de solucionadores rápidos incorporados, capaces de resolver de manera eficiente la mayoría de las clases de modelos de optimización.
Resolver de manera eficiente la mayoría de las clases de modelos de optimización. Aprender acerca del acceso a las herramientas más poderosas de LINGO a través de su lenguaje es una tarea compleja, sin embargo los modelos que no precisan de un complejo uso de recursos pueden resolverse con una sintaxis sumamente sencilla.
Solución de un problema de programación lineal con Lingo
Al igual que para cualquier otro método de resolución, el primer paso para resolver un problema de programación lineal (PL) consiste en el modelamiento matemático, y es en esta fase en la que el profesional de Ingeniería Industrial debe desarrollar su mayor habilidad y destreza. Los pasos para resolver un problema de PL se encuentran en el módulo de programación lineal.
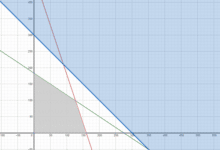
El problema
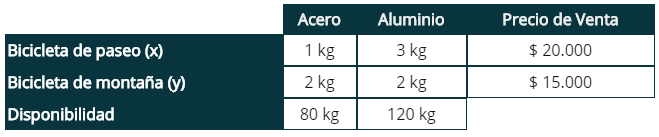
Un herrero con 80 Kg. de acero y 120 Kg. de aluminio quiere hacer bicicletas de paseo y de montaña que quiere vender, respectivamente a 20.000 y 15.000 pesos cada una para sacar el máximo beneficio. Para la de paseo empleará 1 Kg. De acero y 3 Kg. de aluminio, y para la de montaña 2 Kg. de ambos metales. ¿Cuántas bicicletas de paseo y de montaña deberá fabricar para maximizar las utilidades?
El modelo matemático
Declaración de variables
x = Cantidad de bicicletas de paseo a producir
y = Cantidad de bicicletas de montaña a producir
Restricciones de capacidad
Aluminio:
x + 2y <= 80
Acero:
3x + 2y <= 120
Función Objetivo
Zmax = 20000x + 15000y
Ingresando los datos a Lingo
La interfaz de LINGO es quizá la más simple de todas las aplicaciones de resolución de modelos matemáticos, y en el caso de los modelos de programación lineal el ingreso de los datos es muy sencillo, en su ventana inicial es suficiente con utilizar un comando de apertura «MODEL:» y uno de cierre «END», en medio de estos comandos se escribe el modelo tal como mostramos a continuación:
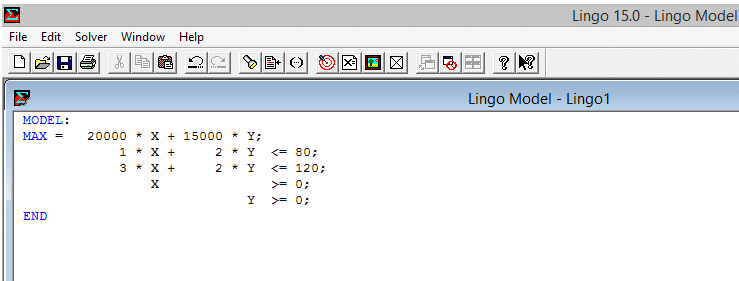
Como podemos observar, el comando «MAX:» se utiliza para consignar la función objetivo y su criterio (en caso de minimizar se utilizará MIN:). Para separar cada línea de código es necesario utilizar el carácter «;». Una vez tenemos el código con nuestras restricciones establecidas, procedemos a resolver, dando clic en el botón Solve:
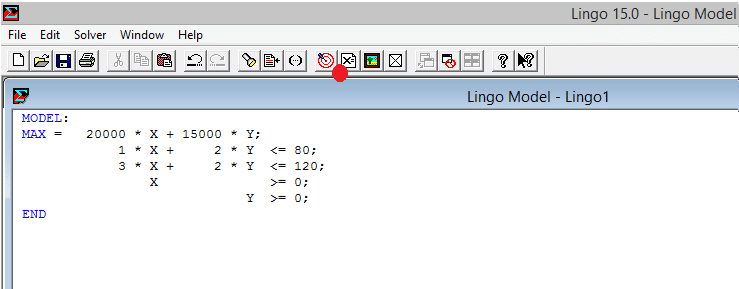
Al resolver obtendremos el reporte solución, con base en sus datos podremos efectuar un análisis de sensibilidad, hay que tener en cuenta que los datos expresados en el reporte se encuentran en función de la línea de código ingresada, por lo tanto hay que considerar en que línea se escribió cada restricción y función objetivo para hacer un adecuado análisis.
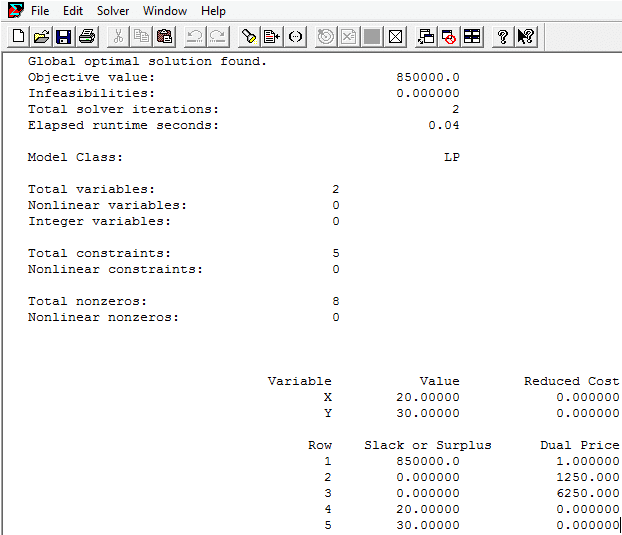
Objective Function: Nos muestra el resultado de nuestra función objetivo, en este caso la solución óptima tiene una función objetivo (utilidad) de $ 850.000.
Value: Es el valor que toman las variables de decisión en la función objetivo.
Dual Price: El precio sombra de una restricción, es el cambio marginal de la función objetivo cuando el valor del lado derecho de la restricción aumenta en una unidad. En nuestro ejemplo sería así: por cada kg de acero adicional que tengamos disponible, la función objetivo aumentará en $ 1250.