El tamaño de la muestra o cálculo de número de observaciones es un proceso vital en la etapa de cronometraje, dado que de este depende en gran medida el nivel de confianza del estudio de tiempos. Este proceso tiene como objetivo determinar el valor del promedio representativo para cada elemento.
Los métodos más utilizados para determinar el número de observaciones son:
- Método Estadístico
- Método Tradicional (Nomográfico)
Método estadístico (OIT)
El método estadístico requiere que se efectúen cierto número de observaciones preliminares (n’), para luego poder aplicar la siguiente fórmula:
NIVEL DE CONFIANZA DEL 95,45% Y UN MÁRGEN DE ERROR DE ± 5%
Siendo:
n = Tamaño de la muestra que deseamos calcular (número de observaciones)
n’ = Número de observaciones del estudio preliminar
Σ = Suma de los valores
x = Valor de las observaciones.
40 = Constante para un nivel de confianza de 95,45%
Ejemplo:
Se realizan 5 observaciones preliminares, los valores de los respectivos tiempos transcurridos en centésimas de minuto son: 8, 7, 8, 8, 7. Ahora pasaremos a calcular los cuadrados que nos pide la fórmula:
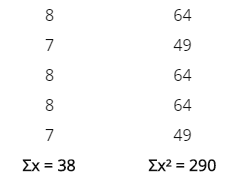
n’ = 5
Sustituyendo estos valores en la fórmula anterior tendremos el valor de n:
Dado que el número de observaciones preliminares (5) es inferior al requerido (7), debe aumentarse el tamaño de las observaciones preliminares, luego recalcular n. Puede ser que en recálculo se determine que la cantidad de 7 observaciones sean suficientes.
Método estadístico (Alternativa)
Por medio de esta fórmula se determina el número de observaciones necesarias para obtener el tiempo de reloj representativo teniendo en cuenta un error porcentual y un nivel de riesgo. Básicamente corresponde a otra metodología sobre la base del método anterior. Cualquier discrepancia en el resultado corresponde a las aproximaciones decimales utilizadas en el método OIT.
La fórmula:
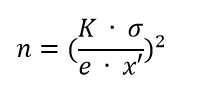
Siendo:
K = El coeficiente de riesgo
El coeficiente de riesgo hace referencia al número de sigmas para asegurar un grado de confianza. Veamos.
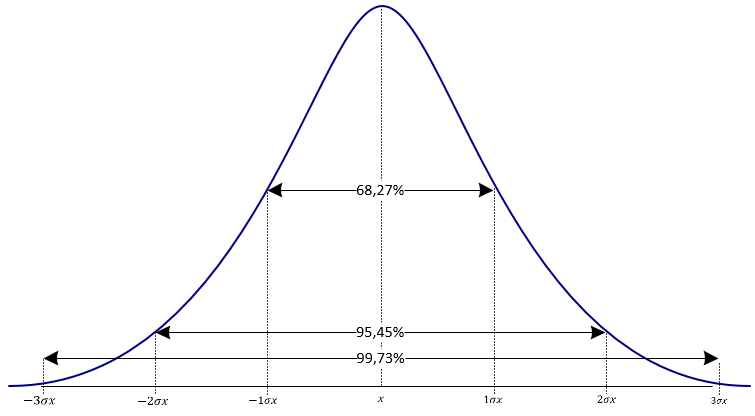
K = 1 para el riesgo de error del 31,73%
K = 2 para el riesgo de error del 4,55%
K = 3 para el riesgo de error del 0,27%
Así entonces, a un nivel de confianza del 95,45% corresponde un k de 2.
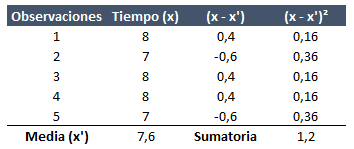
Siendo:
xi = Los valores obtenidos de los tiempos de reloj
x’ = la media aritmética de los tiempos de reloj
σ = Desviación típica de la curva de la distribución
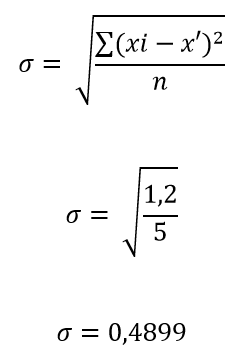
e = error expresado en forma decimal
Para comparar los resultados obtenidos por medio de esta formulación, utilizaremos el mismo margen de error del caso de estudio anterior: +5%. Es decir, se pretende que el 95,45% de las mediciones con cronómetro tengan cuando mucho un 5% de error del dato real (de acuerdo a una distribución normal).
Remplazamos los valores en la fórmula inicial:
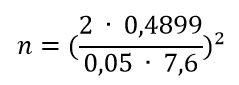
Así podemos observar que ambos métodos conducen al mismo resultado.
Método nomográfico (H.B. Maynard)
Los métodos nomográficos se basan en tablas de referencia. Este método en particular consiste en seguir un procedimiento sistemático desarrollado por H.B Maynard.
1. Realizar una muestra tomando 10 lecturas sí los ciclos son <= 2 minutos y 5 lecturas sí los ciclos son > 2 minutos, esto debido a que hay más confiabilidad en tiempos más grandes, que en tiempos muy pequeños donde la probabilidad de error puede aumentar.
2. Calcular el rango o intervalo de los tiempos de ciclo, es decir, restar del tiempo mayor el tiempo menor de la muestra:
R (Rango) = Xmax – Xmin
3. Calcular la media aritmética o promedio:
Siendo:
Σx = Sumatoria de los tiempos de muestra
n = Número de ciclos tomados
4. Hallar el cociente entre rango y la media:
5. Buscar ese cociente en la siguiente tabla, en la columna (R/X), se ubica el valor correspondiente al número de muestras realizadas (5 o 10) y ahí se encuentra el número de observaciones a realizar para obtener un nivel de confianza del 95% y un nivel de precisión de ± 5%.
Ejemplo
Tomando como base los tiempos contemplados en el ejemplo del método estadístico, abordaremos el cálculo del número de observaciones según el método tradicional.
En primer lugar como el ciclo es inferior a los 2 minutos, se realizan 5 muestras adicionales (6, 8, 8, 7, 8) para cumplir con las 10 muestras para ciclos <= 2 minutos. Las observaciones son las siguientes:
Se calcula el rango:
R (Rango) = 8 – 6 = 2
Ahora se calcula la media aritmética:
Ahora calculamos el cociente entre el rango y la media:
Ahora buscamos ese cociente en la tabla y buscamos su intersección con la columna de 10 observaciones:
Tenemos entonces que el número de observaciones a realizar para tener un nivel de confianza del 95% según el método tradicional es: 11
Al adicionar los 5 tiempos y utilizar el método estadístico tenemos un número de observaciones igual a: 12.8 aproximadamente 13.
Por lo cual podemos concluir que ambos métodos arrojan resultados muy parecidos y que la elección del método se deja a criterio del especialista.
Existen, además, otros métodos como:
- Ábaco de Lifson
- Tabla de Westinghouse
- General Electric
Tengo 2 dudas para el cálculo del número de observaciones con el método estadístico:
#1. En el primer ejemplo dónde se realizaron 5 observaciones y nos dió como resultado 7… ¿Se tienen que realizar 2 observaciones extra a las 5 iniciales o son 7 nuevas observaciones de tiempo.
#2. Una vez que la cantidad de observaciones preliminares es igual al resultado de la fórmula entonces ¿Se tienen que hacer nuevas observaciones o se pueden contemplar las observaciones preliminares?
Agradezco su respuesta a estas dudas y el apoyo que se brinda al compartir esta información.
Tengo las mismas preguntas… recibió respuestas?
¿Qué tal, Christian? no funciona así, la fórmula estadística únicamente nos dice si las muestras fueron suficientes o no partiendo de las lecturas obtenidas, es decir si el valor obtenido al aplicar la fórmula es casi exacto o mayor al número de lecturas preliminar, podemos dejarlo así. Más objetivamente, en ese caso en particular podemos tomar una o cinco mediciones más, complementando las que tenemos y volver a aplicar la fórmula para validar que la cantidad nos de la precisión requerida.
Tengo una consulta con respeto al método tradicional
Como es que logro identificar las observaciones en la tabla, como lo pusieron (6, 8, 8, 7, 8), tomando en cuenta los datos que tengo, les agradecería si me podrían ayudar.
Por que utilizar un nivel de confianza del 95 en este caso?
Para tener un análisis estadístico eficiente se recomienda manejar valores del 90% al 99.9%, menor a esa cantidad no tendría caso ya que el error sería bastante. En teoría normalmente se selecciona la media de ese rango y en la práctica un estudio más preciso es más costoso. ¡Saludos!
Si mis datos no obedecen a una distribución normal, puedo utilizar la formula del método estadistico?
Se utiliza la desviación estandar de la muestra o de la polación?. me parece que se esta usando la de polación y segun literatura no es asi. Podrias confirmar ?