Uso de matrices para definir un modelo de programación lineal en Google OR-Tools
Optimización lineal
Un factor importante al abordar optimización lineal es la eficiencia del modelamiento. En el artículo introductorio a problemas de programación lineal mediante Google OR-Tools, abordamos con fines prácticos, un ejemplo con pocas variables y restricciones.
Cuando el número de variables y restricciones aumenta, se hace necesario contar con herramientas que permitan modelar eficientemente bajo estas condiciones. Una herramienta importante, considerando el modelamiento en lenguajes de programación, consiste en el uso de bucles sobre matrices, que permitan automatizar la definición de variables y restricciones; es decir, pasar de la definición individual de variables a una definición automatizada apoyándose en el uso de matrices.
El objetivo de este artículo consiste en utilizar las librerías del software Google OR-Tools para abordar problemas de programación lineal (optimización lineal) usando matrices para la definición de las variables y restricciones del modelo.
El problema
En el artículo de introducción, abordamos un caso descrito en el libro Applied Mathematical Programming, de Bradley, Hax, and Magnanti (Addison-Wesley, 1977), del MIT (Cápitulo 2 página 50). Con fines prácticos, hemos adaptado dicho modelo, incorporando nuevos procesos al sistema, que impliquen nuevas variables y restricciones:
El propietario de una tienda que produce remolques para automóviles desea determinar la mejor combinación para sus tres productos: remolques de plataforma plana, remolques económicos y remolques de lujo. Su taller se limita a trabajar 24 días al mes en el trabajo de los metales, 60 días al mes en el trabajo de la madera, 40 días al mes en el trabajo de pintura, 50 días al mes en el trabajo de montaje y 45 días al mes en el trabajo de acabados para estos productos. La siguiente tabla indica los datos de producción de los remolques.
Tabla 1
| Uso por cada unidad de tráiler | Recursos disponibles | |||
| Plataforma plana | Económica | Lujosa | ||
| Días de trabajo en metales | 0,5 | 2 | 1 | 24 |
| Días de trabajo en madera | 1 | 2 | 4 | 60 |
| Días de trabajo en pintura | 1,5 | 0,5 | 2 | 40 |
| Días de trabajo en montaje | 1 | 1,5 | 1,5 | 50 |
| Días de trabajo en acabados | 0,5 | 1 | 1,5 | 45 |
| Contribución ($ x 100) | 6 | 14 | 13 | |
Podemos observar, que respecto al problema original, se han incorporado tres procesos más, lo cual implica la adición de nuevas variables y nuevas restricciones.
Modelamiento del problema
Sean las variables de decisión del problema:
x0 = Número de remolques de plataforma plana producidos por mes
x1 = Número de remolques económicos producidos por mes
x2 = Número de remolques de lujo producidos por mes
Suponiendo que los costos de la capacidad de trabajo en metal, madera, pintura, montaje y acabados sean fijos, el problema se convierte en un problema de maximización:
Zmax = 6x0 + 14x1 + 13x2
Sujeto a las siguientes restricciones de capacidad:
0,5x0 + 2x1 + x2 <= 24,
x0 + 2x1 + 4x2 <= 60,
1,5x0 + 0,5x1 + 2x2 <= 40,
1x0 + 1,5x1 + 1,5x2 <= 50,
0,5x0 + 1x1 + 1,5x2 <= 45,
Sujeto a las siguientes restricciones de no-negatividad:
x0 >= 0,
x1 >= 0,
x2 >= 0,
Podemos, del mismo modo, establecer un conjunto de variables que correspondan a las horas ociosas para cada uno de los procesos del sistema (metal, madera, pintura, montaje y acabados):
x3 = Número de horas ociosas en el trabajo en metal al mes,
x4 = Número de horas ociosas en el trabajo en madera al mes,
x5 = Número de horas ociosas en el trabajo en pintura al mes,
x6 = Número de horas ociosas en el trabajo en montaje al mes,
x7 = Número de horas ociosas en el trabajo en acabados al mes,
Reescribimos las restricciones (adicionando las variables de horas ociosas). Podemos observar que las inecuaciones ahora serán igualdades, para que de esta forma ahora podamos tener información relacionada a los recursos. En otras palabras, lo que se utiliza (horas productivas) + lo que sobre (horas ociosas) = tiempo disponible:
0,5x0 + 2x1 + x2 + x3 = 24,
x0 + 2x1 + 4x2 + x4 = 60,
1,5x0 + 0,5x1 + 2x2 + x5 = 40,
1x0 + 1,5x1 + 1,5x2 + x6 = 50,
0,5x0 + 1x1 + 1,5x2 + x7 = 45,
x0 >= 0,
x1 >= 0,
x2 >= 0,
x3 >= 0,
x4 >= 0,
x5 >= 0,
x6 >= 0,
x7 >= 0,
Así entonces, tenemos el problema completamente modelado.
Resolución del modelo mediante Google OR-Tools
Tal como lo hemos mencionado, el objetivo de este artículo es abordar un problema de optimización lineal utilizando matrices para la definición de variables. De tal manera que detallaremos nuevamente cada uno de los pasos utilizados en el modelamiento.
De acuerdo a lo mencionado en el artículo de introducción a Google OR-Tools, esta herramienta soporta múltiples lenguajes de programación, así entonces, haremos uso del lenguaje de programación Python.
Paso 1: Importar la librería
El siguiente fragmento de código importa las librerías necesarias:
# Importar la librería de Google OR-Tools
from ortools.linear_solver import pywraplp
Paso 2: Crear la data del modelo (matrices)
Es recomendable previamente disponer las restricciones por medio de un tabulado que nos permita observar las matrices con claridad. En este caso, la matriz en la cual se relacionan los coeficientes de las restricciones (considerando las variables de horas ociosas), se puede apreciar en la tabla 2.
Tabla 2
| Uso por cada unidad de tráiler | Recursos disponibles | ||||||||
| X0 | X1 | X2 | X3 | X4 | X5 | X6 | X7 | ||
| Metales (días) | 0,5 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 24 |
| Madera (días) | 1 | 2 | 4 | 0 | 1 | 0 | 0 | 0 | 60 |
| Pintura (días) | 1,5 | 0,5 | 2 | 0 | 0 | 1 | 0 | 0 | 40 |
| Montaje (días) | 1 | 1,5 | 1,5 | 0 | 0 | 0 | 1 | 0 | 50 |
| Acabados (días | 0,5 | 1 | 1,5 | 0 | 0 | 0 | 0 | 1 | 45 |
Podemos observar que, en la matriz de entrada de los coeficientes de las restricciones incorporaremos todas las variables, incluso las que no forman parte de la ecuación (incluidas con coeficiente 0), esto para conservar un orden de la matriz.
def create_data_model():
"""Almacena la data de entrada del modelo"""
data = {}
data['restriccion_coef'] = [
[0.5, 2, 1, 1, 0, 0, 0, 0],
[ 1, 2, 4, 0, 1, 0, 0, 0],
[1.5, 0.5, 2, 0, 0, 1, 0, 0],
[ 1, 1.5, 1.5, 0, 0, 0, 1, 0],
[0.5, 1, 1.5, 0, 0, 0, 0, 1],
]
data['limites'] = [24, 60, 40, 50, 45]
data['obj_coef'] = [6, 14, 13, 0, 0, 0, 0, 0]
data['num_vars'] = 8
data['num_restricciones'] = 5
return data- La matriz restriccion_coef contiene todos los coeficientes de la matriz de restricciones.
- La matriz limites contiene todos los valores de la parte derecha de las inecuaciones (límites).
- La matriz obj_coef contiene todos los coeficientes de la función objetivo (los valores en cero representa el peso en la función objetivo de las variables asociadas con las horas ociosas).
Paso 3: Declarar el solucionador y crear las variables del modelo
Haciendo uso de las matrices definidas previamente, el siguiente fragmento de código automatiza la creación de las variables por medio de un bucle:
def main():
data = create_data_model()
# Declara el solucionador GLOP
solver = pywraplp.Solver.CreateSolver('GLOP')
# Crea las variables por medio de un bucle tomando las matrices (data).
infinity = solver.infinity()
x = {}
for j in range(data['num_vars']):
x[j] = solver.IntVar(0, infinity, 'x[%i]' % j)
print('Número de variables =', solver.NumVariables())
Por medio del fragmento anterior se definen cada una de las variables (enteras), y se establecen los límites de cada una de ellas (0, infinity = desde cero hasta el infinito), es decir, hace las veces de restricciones de no-negatividad.
Paso 4: Definir las restricciones del modelo
Haciendo uso de las matrices definidas previamente, el siguiente fragmento de código automatiza la definición de las restricciones por medio de un bucle:
for i in range(data['num_restricciones']):
constraint = solver.RowConstraint(data['limites'][i], data['limites'][i], '')
for j in range(data['num_vars']):
constraint.SetCoefficient(x[j], data['restriccion_coef'][i][j])
print('Número de restricciones =', solver.NumConstraints())
Usando el método RowConstraint creamos las restricciones de manera automatizada para el modelo. Los signos de las inecuaciones o igualdades (límites) se expresan dentro del método. Citaremos algunos ejemplos:
- Inecuación mayor o igual a: solver.RowConstraint(data[‘limites’][i], infinity, »)
- Inecuación menor o igual a: solver.RowConstraint(0, data[‘limites’][i], »)
- Igualdad,ecuación igual a: solver.RowConstraint(data[‘limites’][i], data[‘limites’][i], »)
La expresión data[‘limites][i] toma el valor correspondiente al límite asociado a la fila de cada restricción (fila i) desde la matriz límites. Así entonces, y tomando como ejemplo la primera restricción (fila 0, es decir i =0), lo que expresaría el código en cada caso sería:
- Inecuación mayor o igual a: valores desde 24 hasta el infinito (>= 24)
- Inecuación menor o igual a: valores desde 0 hasta el 24 (<= 24)
- Igualdad, ecuación igual a: valores desde 24 hasta 24 (= 24)
Paso 5: Definir la función objetivo del modelo
Haciendo uso de las matrices definidas previamente, el siguiente fragmento de código automatiza la definición de la función objetivo por medio de un bucle (maximizar):
objective = solver.Objective()
for j in range(data['num_vars']):
objective.SetCoefficient(x[j], data['obj_coef'][j])
objective.SetMaximization()
Paso 6: Invocar el solucionador
El siguiente fragmento de código sirve para invocar el solucionador del modelo:
status = solver.Solve()
Paso 7: Definir las salidas del solucionador
De acuerdo a los bucles definidos, las variables toman los nombres base siguiendo el formato x[i]; de manera que por medio del siguiente código, renombraremos las variables para una mejor comprensión de las salidas del solucionador.
print('Valor objetivo =', solver.Objective().Value())
print('Solución:')
print('Remolques de plataforma plana producidos por mes =', x[0].solution_value())
print('Remolques económicos producidos por mes =', x[1].solution_value())
print('Remolques de lujo producidos por mes =', x[2].solution_value())
print('Horas ociosas en el trabajo en metal al mes =', x[3].solution_value())
print('Horas ociosas en el trabajo en madera al mes =', x[4].solution_value())
print('Horas ociosas en el trabajo en pintura al mes =', x[5].solution_value())
print('Horas ociosas en el trabajo en montaje al mes =', x[6].solution_value())
print('Horas ociosas en el trabajo en acabados al mes =', x[7].solution_value())
print()
print('Problema resuelto en %f milisegundos' % solver.wall_time())
print('Problema resuelto en %d iteraciones' % solver.iterations())
else:
print('El problema no tiene solución óptima.')
Es posible que el desarrollo de los siete pasos anteriores demande algún grado de complejidad subyacente del uso de un lenguaje de programación; sin embargo, es preciso mencionar que, el modelo anterior queda perfectamente configurado, y puede replicarse con modificaciones menores en múltiples problemas de optimización lineal. Ahora bien, haciendo el uso de matrices, se puede mejorar considerablemente la eficiencia del modelamiento.
¿Cómo ejecutar el modelo?
Lo primero que debemos considerar, es que es preciso contar con la instalación de Python en nuestro equipo de cómputo, así mismo debemos contar con la última versión del comando pip y por supuesto, el software OR-Tools. Una guía detallada de la instalación de estos requerimientos la podrás encontrar en el siguiente enlace:
Instalación de OR-Tools para Python
Ahora, lo recomendable es trabajar con algún editor de código práctico, por ejemplo: Sublime Text.
En este caso, haremos uso del editor Sublime Text, al cual llevaremos íntegramente el código completo del programa:
#Caso desde: Bradley, Hax, and Magnanti,
#'Applied Mathematical Programming', Chapter 2
#Nuevos procesos adicionados por Salazar (2021)
# Importar la librería de Google OR-Tools
from ortools.linear_solver import pywraplp
def create_data_model():
"""Almacena la data de entrada del modelo"""
data = {}
data['restriccion_coef'] = [
[0.5, 2, 1, 1, 0, 0, 0, 0],
[ 1, 2, 4, 0, 1, 0, 0, 0],
[1.5, 0.5, 2, 0, 0, 1, 0, 0],
[ 1, 1.5, 1.5, 0, 0, 0, 1, 0],
[0.5, 1, 1.5, 0, 0, 0, 0, 1],
]
data['limites'] = [24, 60, 40, 50, 45]
data['obj_coef'] = [6, 14, 13, 0, 0, 0, 0, 0]
data['num_vars'] = 8
data['num_restricciones'] = 5
return data
def main():
data = create_data_model()
# Declara el solucionador GLOP
solver = pywraplp.Solver.CreateSolver('GLOP')
# Crea las variables por medio de un bucle tomando las matrices (data).
infinity = solver.infinity()
x = {}
for j in range(data['num_vars']):
x[j] = solver.IntVar(0, infinity, 'x[%i]' % j)
print('Número de variables =', solver.NumVariables())
# Definir las restricciones por medio de un bucle tomando las matrices (data).
for i in range(data['num_restricciones']):
constraint = solver.RowConstraint(data['limites'][i], data['limites'][i], '')
for j in range(data['num_vars']):
constraint.SetCoefficient(x[j], data['restriccion_coef'][i][j])
print('Número de restricciones =', solver.NumConstraints())
# Define la función objetivo por medio de un bucle tomando las matrices (data).
objective = solver.Objective()
for j in range(data['num_vars']):
objective.SetCoefficient(x[j], data['obj_coef'][j])
objective.SetMaximization()
# In Python, you can also set the objective as follows.
# obj_expr = [data['obj_coeffs'][j] * x[j] for j in range(data['num_vars'])]
# solver.Maximize(solver.Sum(obj_expr))
status = solver.Solve()
if status == pywraplp.Solver.OPTIMAL:
print('Valor objetivo =', solver.Objective().Value())
print('Solución:')
print('Remolques de plataforma plana producidos por mes =', x[0].solution_value())
print('Remolques económicos producidos por mes =', x[1].solution_value())
print('Remolques de lujo producidos por mes =', x[2].solution_value())
print('Horas ociosas en el trabajo en metal al mes =', x[3].solution_value())
print('Horas ociosas en el trabajo en madera al mes =', x[4].solution_value())
print('Horas ociosas en el trabajo en pintura al mes =', x[5].solution_value())
print('Horas ociosas en el trabajo en montaje al mes =', x[6].solution_value())
print('Horas ociosas en el trabajo en acabados al mes =', x[7].solution_value())
print()
print('Problema resuelto en %f milisegundos' % solver.wall_time())
print('Problema resuelto en %d iteraciones' % solver.iterations())
else:
print('El problema no tiene solución óptima.')
if __name__ == '__main__':
main()Es necesario que el editor esté configurado de acuerdo a la sintaxis de Python y el archivo se guarde como tal, con la extensión .py.
Lo siguiente será ejecutar el código, para eso podemos utilizar la consola del sistema (símbolo del sistema) o CMD. En ella, debemos dirigirnos hacia el directorio en el cual se encuentre nuestro archivo .py y ejecutarlo de la siguiente manera:
python Nombre del archivo.py
En nuestro caso, hemos guardado el modelo como PL_matrix.py, así que de esa manera lo ejecutamos desde la consola del sistema:
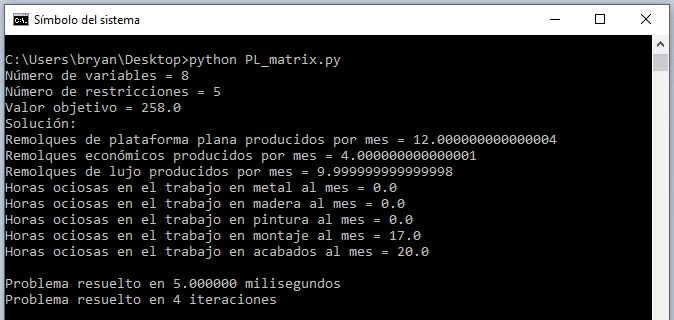
Y bien, tenemos la solución a este problema de programación lineal en 5 milisegundos (varía de acuerdo a las especificaciones del equipo) y en 4 iteraciones.
Dada la adición de variables de holgura o exceso, podemos identificar que existen dos restricciones redundantes: Horas montaje y horas de acabados.
Ahora bien, el modelo de optimización lineal y el script del solucionador quedaron desarrollados en un lenguaje de programación estándar y ampliamente utilizado. Desde luego, las posibilidades de integrar datos de entrada y procesar los datos de salidas son interesantes. Por ejemplo, es posible desarrollar un script mediante el cual el código ya desarrollado tome las matrices de entrada desde un archivo de Excel, o desde archivo csv.
Podemos observar que las variables que forman parte de la solución toman valores continuos, y dado el caso práctico, no es ajustado a la realidad mencionar que se producirán 9,99 remolques de lujo. De manera que, en próximos artículos abordaremos la solución de problemas de programación lineal entera y mixta (optimización lineal entera y mixta MIP), ya que Google OR-Tools cuenta con un solucionador específico para abordar este tipo de modelos.