Problema de la ruta más corta en Google OR-Tools
El problema del flujo de costo mínimo
Podemos decir que el problema o algoritmo de la ruta más corta es una popularización del problema del flujo del costo mínimo, una variación de los modelos generales de flujos. Cuando nos referimos al costo mínimo, este en realidad puede expresarse en diversas magnitudes: distancia, tiempo, volumen, y en general, cual cualquier unidad que represente el caso de estudio.
En el problema del flujo de costo mínimo, cada arco de la red tiene un costo asociado a transportar unidades a través de él, es decir, por ejemplo, que el arco que une a los nodos 0 y 1, tiene un costo subyacente a su transporte, en los términos que representen mejor al modelo. Además del costo, cada arco debe considerar una capacidad de transporte.
Del mismo modo, debe considerarse que en este problema los nodos tienen una naturaleza, y existen algunos nodos especiales:
- nodos de oferta: puntos desde los cuales se suministran unidades de flujo (fuentes)
- nodos de demanda: puntos hacia los cuales se llevan unidades de flujo para su consumo, sumidero o hundimiento (destinos)
- nodos neutrales: puntos a través de los cuales pasan unidades de flujo, no genera nuevas unidades, no consume unidades, son puntos de tránsito.
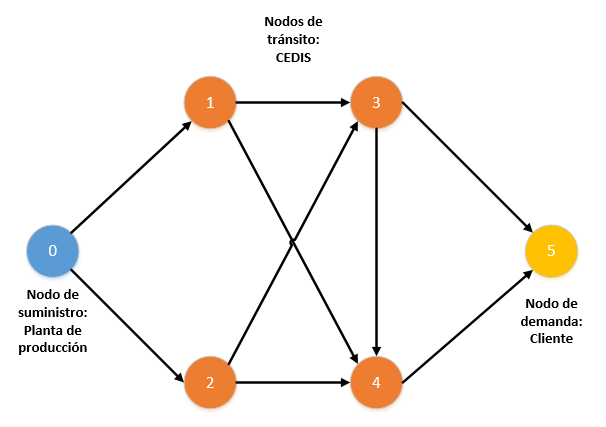
En el anterior gráfico se puede apreciar una representación básica de lo que sería la naturaleza de los nodos aplicada a un caso común: una planta que produce material, lo envía hacia algunos centros de distribución o consolidación y un cliente, lugar que representa el destino final del material. Claramente pueden apreciarse cuales son los nodos de oferta, de demanda y de tránsito. Ahora bien, es posible que en la práctica existan múltiples nodos de oferta y múltiples nodos de demanda, del mismo modo, es posible que los nodos de tránsito también suministren o consuman unidades, lo que los convertiría en nodos mixtos, y lo que podría representar múltiples casos prácticos, por ejemplo: un centro de distribución ubicado en una planta, el cual recibe unidades para consumo interno y despacha excedentes hacia otros centros o clientes.
Problema de la ruta más corta
Tal como se mencionó en la introducción del artículo, el problema de la ruta más corta puede abordarse desde la perspectiva del problema del flujo de costo mínimo, en el cual el objetivo consiste en determinar el plan de rutas que genere la trayectoria con la mínima distancia total, que una un nodo fuente (puro) con un nodo destino (puro), sin importar el número de nodos que existan entre estos.
Así entonces, en su versión más básica, el flujo y la capacidad de los arcos puede reducirse a la unidad (1), asumiendo que no se transportan materiales y que el único objetivo que se persigue consiste en determinar la ruta más corta que une a un nodo fuente con un nodo destino. Dicho de otro modo, el nodo fuente produce una unidad que es transportada por medio de arcos con capacidad de unidad y se consume en la medida de una unidad en el nodo destino.
Es preciso reiterar que cuando nos referimos distancia nos ajustamos al nombre del algoritmo «la ruta más corta», sin embargo, lo que se considera distancia, bien puede expresarse en otras unidades de medida, por ejemplo: costo.
El objetivo de este artículo consiste en utilizar las librerías del software Google OR-Tools para abordar el problema de la ruta más corta a través de una interfaz base del algoritmo del flujo de costo mínimo. Posteriormente, abordaremos un script básico en Python que nos permita integrar al modelo de optimización, data de entrada proveniente de fuentes como un documento de Excel.
El problema
Con el propósito de evaluar los resultados obtenidos mediante distintos métodos y solucionadores, utilizaremos el mismo problema que abordamos mediante programación lineal y el módulo de network modeling de WinQSB.
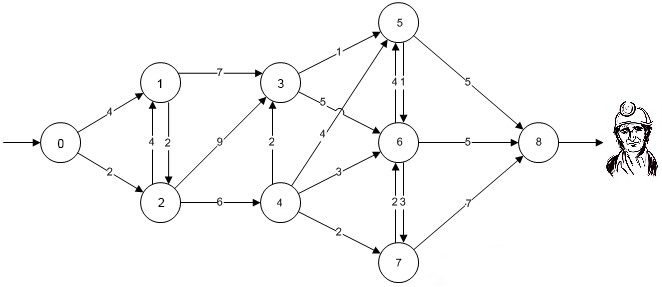
Un minero ha quedado atrapado en una mina, la entrada a la mina se encuentra ubicada en el nodo 0, se conoce de antemano que el minero permanece atrapado en el nodo 8, para llegar a dicho nodo hay que atravesar una red de túneles que van conectados entre sí. El tiempo de vida que le queda al minero sin recibir auxilio es cada vez menor y se hace indispensable hallar la ruta de acceso al nodo 8 más corta. Las distancias entre nodos de la mina se encuentran en la siguiente gráfica dadas en cientos de metros:
Resolviendo un problema de la ruta más corta mediante Google OR-Tools
De acuerdo a lo mencionado en el artículo de introducción a Google OR-Tools, esta herramienta soporta múltiples lenguajes de programación, así entonces, haremos uso del lenguaje de programación Python.
Es posible que para la ejecución de este script, debas instalar el comando future, el cual puedes encontrar en el siguiente enlace: future 0.18.2. La instalación es muy simple, tan solo escribir en el cmd (símbolo del sistema) lo siguiente:
pip install future
Paso 1: Importar la librería
El siguiente fragmento de código importa las librerías necesarias:
# Importar la librería de Google OR-Tools
from __future__ import print_function
from ortools.graph import pywrapgraphPaso 2: Crear la data del modelo
Define cuatro matrices paralelas: nodos_fuente, nodos_destino, capacidades, y costos_unitarios, entre cada par. Por ejemplo, el arco desde el nodo 0 hacia el nodo 1 tiene una capacidad de 1 y un costo asociado de 4 (distancia). En su versión más básica el objetivo consiste en unir un nodo fuente y un nodo destino; por esta razón, en este ejemplo la capacidad de todos los nodos equivale a 1 y el flujo es binario, donde tomará valores de 1 en el caso en que el arco forme parte del conjunto solución y 0 en el caso contrario:
Pueden observarse las matrices perfectamente alineadas, ya que el orden es importante. El orden entre la matriz de nodos_fuente y nodos_destino definirá el valor de los arcos del modelo (distancia).
nodos_fuente = [ 0, 0, 1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 5, 5, 6, 6, 6, 7, 7]
nodos_destino = [ 1, 2, 2, 3, 1, 3, 4, 5, 6, 3, 6, 7, 6, 8, 5, 7, 8, 6, 8]
capacidades = [ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
distancia = [ 4, 2, 2, 7, 4, 9, 6, 1, 5, 2, 3, 2, 1, 5, 4, 3, 6, 2, 6]
suministros = [1, 0, 0, 0, 0, 0, 0, 0, -1]También definimos la matriz de suministros asociada a los nodos, donde los valores positivos corresponde a oferta y los valores positivos corresponde a demanda. Los ceros se asocian a los nodos de tránsito. En nuestro ejemplo solo existe un nodo de oferta = nodo 0, y un nodo de demanda = nodo 8.
Paso 3: Declarar el solucionador y agregar los arcos del modelo
El siguiente fragmento define en primera instancia el solucionador (declara). Luego, define cada arco del problema, es decir, con base en las matrices definidas como datos de entrada (en su orden), establece el valor (costo = distancia) de cada arco. Posteriormente, define los suministros (o demandas) para cada nodo.
# Crea una instancia para el solucionador
min_cost_flow = pywrapgraph.SimpleMinCostFlow()
# Define cada arco del problema
for i in range(0, len(nodos_fuente)):
min_cost_flow.AddArcWithCapacityAndUnitCost(nodos_fuente[i], nodos_destino[i],
capacidades[i], distancia[i])
# Define los suministros para cada nodo.
for i in range(0, len(suministros)):
min_cost_flow.SetNodeSupply(i, suministros[i])
Paso 4: Invocar al solucionador y definir la información de salida del modelo
El siguiente fragmento de código utiliza las librerías predeterminadas de Google OR-Tools para abordar problemas de flujo de costo mínimo. Así mismo, se especifican las salidas del solucionador: arco / flujo / capacidad / distancia, para cada arco; y distancia total de la red.
# Encuentra el costo mínimo entre el nodo 0 y el nodo 8
if min_cost_flow.Solve() == min_cost_flow.OPTIMAL:
print('Distancia mínima:', min_cost_flow.OptimalCost())
print('')
print(' Arco Flujo / Capacidad Distancia')
for i in range(min_cost_flow.NumArcs()):
cost = min_cost_flow.Flow(i) * min_cost_flow.UnitCost(i)
print('%1s -> %1s %3s / %3s %3s' % (
min_cost_flow.Tail(i),
min_cost_flow.Head(i),
min_cost_flow.Flow(i),
min_cost_flow.Capacity(i),
cost))
else:
print('Hubo un problema con la entrada de flujo de distancia mínima.')
Es posible que el desarrollo de los cuatro pasos anteriores demande algún grado de complejidad subyacente del uso de un lenguaje de programación; sin embargo, es preciso mencionar que, el modelo anterior queda perfectamente configurado, y puede replicarse con modificaciones menores en múltiples problemas de asignación.
¿Cómo ejecutar el modelo?
Alternativa 1, ejecución en nuestro equipo:
Lo primero que debemos considerar, en el caso de que queramos ejecutar este código en nuestro equipo, es que es preciso contar con la instalación de Python en nuestro equipo de cómputo, así mismo debemos contar con la última versión del comando pip y por supuesto, el software OR-Tools. Una guía detallada de la instalación de estos requerimientos la podrás encontrar en el siguiente enlace:
Instalación de OR-Tools para Python
Ahora, lo recomendable es trabajar con algún editor de código práctico (IDE), por ejemplo: Sublime Text, o Spyder (Una herramienta más completa y por ende más robusta y pesada).
Alternativa 2, ejecución en un entorno virtual (Recomendado):
Podemos utilizar del mismo modo, un entorno virtual. En este caso recomendamos el uso de Colaboratory de Google, un entorno que cuenta con todas las herramientas necesarias para nuestros desarrollos. No tendremos que instalar nada en nuestro equipo, y aprovecharemos la potencia de las máquinas de Google.
El código completo de nuestro desarrollo lo presentamos a continuación. También puedes ver el cuaderno de este módulo en nuestro Colaboratory: Ruta más corta.
#Desde: Salazar, ingenieriaindustrialonline.com - Algoritmo de la ruta más corta
from __future__ import print_function
from ortools.graph import pywrapgraph
def main():
"""MinCostFlow adaptado a la ruta más corta - interfaz de ejemplo."""
# Define cuatro matrices paralelas: nodos_fuente, nodos_destino,
# capacidades, y costos_unitarios entre cada par.
nodos_fuente = [ 0, 0, 1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 5, 5, 6, 6, 6, 7, 7]
nodos_destino = [ 1, 2, 2, 3, 1, 3, 4, 5, 6, 3, 6, 7, 6, 8, 5, 7, 8, 6, 8]
capacidades = [ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
distancia = [ 4, 2, 2, 7, 4, 9, 6, 1, 5, 2, 3, 2, 1, 5, 4, 3, 6, 2, 6]
# Define una matriz con los suministros de cada nodo (valores positivos =
# suministros) y (valores negativos = demandas)
suministros = [1, 0, 0, 0, 0, 0, 0, 0, -1]
# Crea una instancia para el solucionador
min_cost_flow = pywrapgraph.SimpleMinCostFlow()
# Define cada arco del problema
for i in range(0, len(nodos_fuente)):
min_cost_flow.AddArcWithCapacityAndUnitCost(nodos_fuente[i], nodos_destino[i],
capacidades[i], distancia[i])
# Define los suministros para cada nodo.
for i in range(0, len(suministros)):
min_cost_flow.SetNodeSupply(i, suministros[i])
# Encuentra el costo mínimo entre el nodo 0 y el nodo 8
if min_cost_flow.Solve() == min_cost_flow.OPTIMAL:
print('Distancia mínima:', min_cost_flow.OptimalCost())
print('')
print(' Arco Flujo / Capacidad Distancia')
for i in range(min_cost_flow.NumArcs()):
cost = min_cost_flow.Flow(i) * min_cost_flow.UnitCost(i)
print('%1s -> %1s %3s / %3s %3s' % (
min_cost_flow.Tail(i),
min_cost_flow.Head(i),
min_cost_flow.Flow(i),
min_cost_flow.Capacity(i),
cost))
else:
print('Hubo un problema con la entrada de flujo de distancia mínima.')
if __name__ == '__main__':
main()
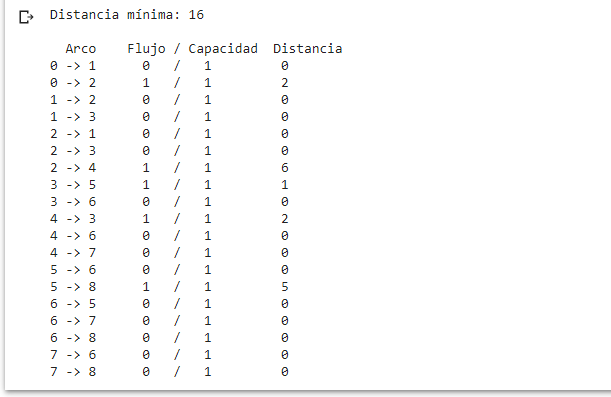
Y bien, tenemos la solución a este problema simple de asignación en menos de 1 segundo.
Podemos observar que se ha obtenido la misma respuesta que la lograda mediante programación lineal y el módulo de network modeling de WinQSB:
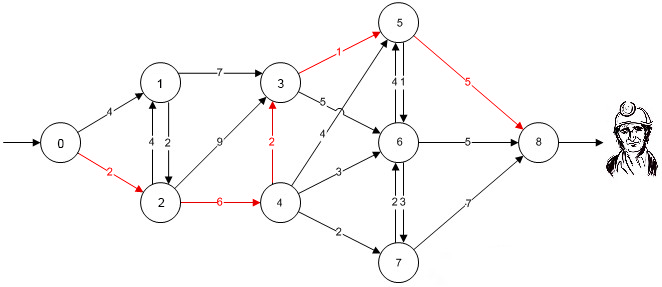
Problema de la ruta más corta mediante Google OR-Tools, importando los datos desde Excel
Tal como lo planteamos al inicio del artículo, abordaremos un script básico en Python que nos permita integrar al modelo de optimización, data de entrada proveniente de fuentes como un documento de Excel. Esto con el propósito de introducirnos en las bondades del modelamiento en lenguajes de programación.
Paso 1: Construir una base de datos en Microsoft Excel
En este caso, utilizaremos una hoja de cálculo haciendo uso de Microsoft Excel, en su extensión predeterminada xlsx, desde la cual, construiremos una base de datos que consignará toda la información de entrada relacionada con el modelo. Un consejo práctico, es que este archivo se guarde dentro del mismo directorio en el que se encuentra el modelo desarrollado en Python.
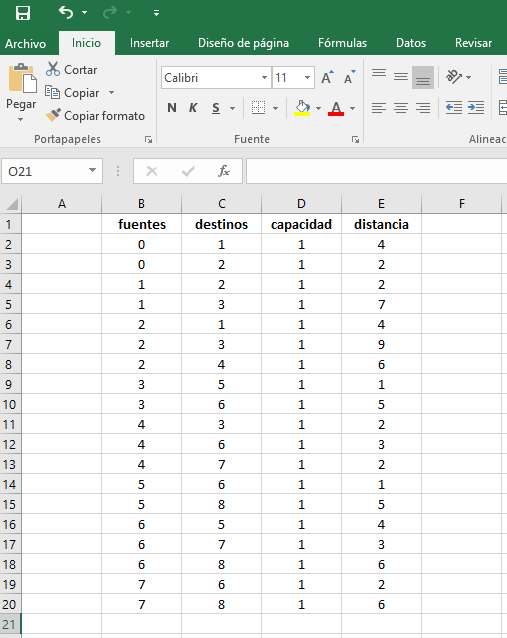
Se puede apreciar la forma en la cual hemos consignado la información, desde luego, respetando el orden de los datos, ya que, tal como lo mencionamos, es muy importante, ya que de ello depende la asociación de cada arco con su distancia. La anterior información la hemos consignado en la Hoja 1 del archivo, ya que en la Hoja 2 consignaremos la información relacionada con el suministros (con el objetivo práctico de mostrar cómo se importan datos desde hojas específicas), de esta manera:
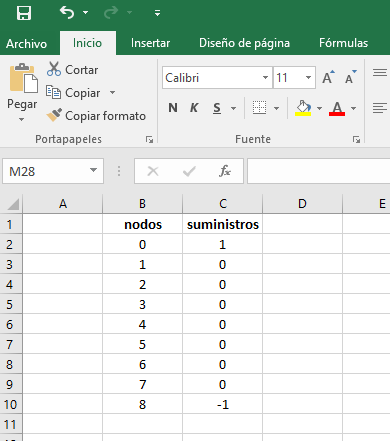
Del mismo modo, el orden de los suministros es muy importante, razón por la cual hemos construido una columna denominada nodos que puede servir como guía para consignar la información de los suministros de forma ordenada.
Es de vital importancia, nombrar cada columna y tener claridad sobre ello, desaconsejamos el uso de caracteres especiales y sugerimos utilizar nombres cortos relacionados con la información contenida.
Posterior a consignar la información, podemos guardar el documento, en este caso lo hemos nombrado: data_flujo. Este dato es importante, ya que lo utilizaremos desde el script.
Paso 2: Importar la librería Pandas
En caso de requerir la instalación de la librería, tan solo debes escribir el siguiente comando en el símbolo del sistema:
pip install pandas
Esta paquete nos proporcionará la posibilidad de importar y trabajar con datos de fuentes como Microsoft Excel. El siguiente fragmento de código se adicionará al script e importará la librería:
# Importar la librería de Google OR-Tools
# Importar la librería de Pandas
from __future__ import print_function
from ortools.graph import pywrapgraph
import pandas as pdUna vez que importemos la librería, podemos trabajar con sus funciones.
Paso 3: Importar datos desde Microsoft Excel
El desarrollo para importar la información desde Excel debe estar correctamente ordenada (correspondencia entre filas). Por ejemplo:
| fila | fuentes | destinos | capacidad | distancia |
| 1 | 0 | 1 | 1 | 4 |
La anterior fila representa el arco entre el nodo 0 y el nodo 1 cuya capacidad es de 1 y de dimensión (distancia) 4.
En el caso de los suministros, debe considerarse el orden la columna en Excel. Por ejemplo:
| fila | nodos | suministros |
| 1 | 0 | 1 |
| 5 | 4 | 0 |
| 9 | 8 | -1 |
En este caso, el nodo 0 será de oferta, es decir, desde ahí se crea flujo; el nodo 8 será de demanda, es decir, en este nodo se consume (sumidero). El nodo 4 será un nodo de tránsito (no crea inicia flujo ni lo consume), solo es un nodo de paso.
El siguiente fragmento de código importará la data que se encuentra consignada en el documento de Excel:
def create_data():
excel = pd.read_excel('data_flujo.xlsx')
excel_1 = pd.read_excel('data_flujo.xlsx', sheet_name=1)
data = {}
data['fuentes'] = excel['fuentes'].tolist()
data['destinos'] = excel['destinos'].tolist()
data['capacidad'] = excel['capacidad'].tolist()
data['distancias'] = excel['distancia'].tolist()
data['suministro'] = excel_1['suministros'].tolist()
return data Los datos de entrada del modelo los trataremos dentro de una función create_data, desde ahí utilizaremos algunas funciones de la librería Pandas (pd) para disponer correctamente de la información contenida en el documento de Excel. Veamos cómo:
excel = pd.read_excel(‘data_flujo.xlsx’)
En este caso, creamos la variable excel y dentro de ella utilizamos la función read_excel la cual permite leer el documento de Excel (en nuestro caso data_flujo.xlsx), e importarlo (en la variable excel) en formato dataframe (conjunto de columnas).
También creamos la variable excel_1 y dentro de ella utilizamos la función read_excel la cual permite leer el documento de Excel (en nuestro caso data_flujo.xlsx), e importarlo (en la variable excel). En este caso adicionamos el argumento sheet_name, el cual nos permite dentro del documento buscar la información en una hoja específica. Las hojas de Excel, en el caso de Python, se denominan desde el índice 0. Es decir que en nuestro caso, al expresar sheet_name=1 indicamos que lea la Hoja 2 del documento.
Creamos el directorio data, temporalmente vacío, en el se consignarán posteriormente cada lista de datos junto a su nombre (índice).
Ahora detallaremos cómo creamos cada listado de datos:
data[‘fuentes’] = excel[‘fuentes’].tolist()
En este caso data[‘fuentes’] indica que crearemos el índice ‘fuentes’ dentro del directorio data (que se encontraba vacío). excel[‘fuentes’] indica que dentro del dataframe Excel, queremos obtener la columna ‘fuentes’. Y la función tolist() convertirá esta columna en una lista (formato list). En defintiva, dentro de data[‘fuentes’] tendremos el listado de fuentes obtenido desde Excel.
Este mismo procedimiento lo repetimos para los datos restantes. Al finalizar, dentro del directorio data quedará contenida toda la información de entrada del modelo. Como la función create_data retorna la variable data, esto quiere decir, que toda la información de entrada quedará contenida dentro de la función create_data, esto permitirá su uso posterior.
Paso 4: Invocar la data del modelo en el main
Para utilizar los listados o inputs obtenidos desde Excel, necesitamos invocar la función «create_data» esta retornará el directorio con todos los datos.
Recomendamos utilizar el mismo nombre «data» para crear el directorio dentro de esta función:
data = create_data()
Ahora el «data» de esta función (main), contiene el directorio de la función «create_data«. Ya podemos usar los listados.
Quiere decir esto, que para acceder específicamente al listado que contiene los destinos, por ejemplo, es necesario invocar a data[‘destinos’].
Básicamente, estas son las modificaciones que deben realizarse sobre el modelo inicialmente desarrollado. De esta forma quedará nuestro código completo, el cual importará la data de entrada desde un archivo de Excel:
# """From Salazar, ingenieriaindustrialonline.com - Algoritmo de la ruta más corta"""
from __future__ import print_function
from ortools.graph import pywrapgraph #Librería de Google Or Tools
import pandas as pd #Librería pandas para obtener data desde Excel
"""MinCostFlow adaptado a la ruta más corta - interfaz de ejemplo."""
#Este desarrollo requiere que la información extraida desde Excel esté ordenada
#de acuerdo a sus filas. Por ejemplo:
#fila fuentes destinos capacidad distancia
# 1 0 1 1 4
#Esta fila representa el arco de capacidad 1 y distancia 4 que conecta el nodo fuente 0
#al nodo destino 1
#En el caso de los suministros, debe considerarse el orden de la columna de Excel. Por ejemplo:
#fila nodos suministros
# 1 0 1
# 5 4 0
# 9 8 -1
#En este caso, el nodo 0 será de oferta (desde ahí se crea flujo) y el nodo 8 será de demanda (ahí se consume).
#El nodo 4 será un nodo de tránsito (no crea flujo y no consume), solo es un nodo de paso.
#Creamos la data del modelo (La extraemos desde Excel)
def create_data():
#La variable "excel" traerá la información contenida en el archivo "data_flujo.xlsx" (crea un dataframe organizado en columnas)
excel = pd.read_excel('data_flujo.xlsx')
excel_1 = pd.read_excel('data_flujo.xlsx', sheet_name=1) #Función que permite leer una hoja en específico (hoja 2 de Excel - Inicia desde 0)
data = {} #Crea un directorio llamado data, en él agregaremos cada lista de datos junto con su nombre (índice)
#La información contenida en Excel viene dada en un dataframe con todos los datos en columnas.
#A continuación, extraeremos cada columna en específico, desde el dataframe (todas las columnas) > series (columna en específico)
#Luego, el "tolist" convertirá cada serie en una lista. Esa lista se guardará en el directorio "data" y se etiqueta con el índice correspondiente
data['fuentes'] = excel['fuentes'].tolist() #Columna en Excel = 'fuentes' > lista en el directorio "data" con la etiqueta (índice) "fuentes"
data['destinos'] = excel['destinos'].tolist() #Columna en Excel = 'destinos' > lista en el directorio "data" con la etiqueta (índice) "destinos"
data['capacidad'] = excel['capacidad'].tolist() #Columna en Excel = 'capacidad' > lista en el directorio "data" con la etiqueta (índice) "capacidad"
data['distancias'] = excel['distancia'].tolist() #Columna en Excel = 'distancia' > lista en el directorio "data" con la etiqueta (índice) "distancia"
data['suministro'] = excel_1['suministros'].tolist() #Columna en Excel = 'suministro' > lista en el directorio "data" con la etiqueta (índice) "suministro"
#Quiere decir esto, que para acceder específicamente al listado que contiene los destinos, es necesario invocar a data['destinos'].
return data #En "create_data" quedará contenido el directorio "data" el cuál contiene todas las listas con la información del modelo.
def main():
#Para utilizar los listados o inputs obtenidos desde Excel, necesitamos invocar la función "create_data" esta retornará el directorio con todos los datos.
#Recomendamos utilizar el mismo nombre "data" para crear el directorio dentro de esta función:
data = create_data() #Ahora el "data" de esta función, contiene el directorio de la función "create_data". Ya podemos usar los listados.
# Crea una instancia para el solucionador
min_cost_flow = pywrapgraph.SimpleMinCostFlow()
# Define cada arco del problema
for i in range(0, len(data['fuentes'])):
min_cost_flow.AddArcWithCapacityAndUnitCost(data['fuentes'][i], data['destinos'][i],
data['capacidad'][i], data['distancias'][i])
# Define los suministros para cada nodo.
for i in range(0, len(data['suministro'])):
min_cost_flow.SetNodeSupply(i, data['suministro'][i])
# Encuentra el costo mínimo entre el nodo 0 y el nodo 8
if min_cost_flow.Solve() == min_cost_flow.OPTIMAL:
print('Distancia mínima:', min_cost_flow.OptimalCost())
print('')
print(' Arco Flujo / Capacidad Distancia')
for i in range(min_cost_flow.NumArcs()):
cost = min_cost_flow.Flow(i) * min_cost_flow.UnitCost(i)
print('%1s -> %1s %3s / %3s %3s' % (
min_cost_flow.Tail(i),
min_cost_flow.Head(i),
min_cost_flow.Flow(i),
min_cost_flow.Capacity(i),
cost))
else:
print('Hubo un problema con la entrada de flujo de distancia mínima.')
if __name__ == '__main__':
main()
Ejecutamos el modelo:

De esta manera hemos logrado integrar una base de datos que se encuentra en un archivo de Excel, el cual podemos modificar en cualquier momento con suma facilidad; un modelo de optimización flexible basado en el algoritmo de flujos de costo mínimo y un solucionador potente. Así entonces, podemos con suma eficiencia, modelar problemas relacionados con el Algoritmo de la Ruta más corta.
En próximos artículos abordaremos algunos scripts básicos en Python que nos permitan exportar los resultados del solucionador en algún formato específico, y de acuerdo a una estructura definida.