Efecto de la variabilidad en el Balance de líneas a través de Simulación
Hemos podido analizar la base teórica que refuta al balanceo de líneas como herramienta para gestionar el flujo de una línea de producción. Los conceptos de interdependencia y variabilidad afectan considerablemente los estimados determinísticos de esta popular herramienta de la gestión de operaciones. En los artículos: Refutación al balanceo de líneas y La planta desbalanceada se profundiza en ello.
El objetivo de este artículo consiste en evaluar los efectos de producción de una línea desbalanceada desde la base (mediante ejemplo clásico de línea de producción); luego evaluar su rendimiento de acuerdo a la intervención de la herramienta determinística del balance de líneas; por último, considerar la variabilidad de cada proceso para evaluar el efecto de la misma en una línea teóricamente balanceada. Para esto utilizaremos simulación, específicamente utilizaremos Bizagi.
Caso de ejemplo
Asumamos un proceso secuencial que consta de 5 operaciones:

Con base en un estudio de tiempos (con 50 observaciones por operación), el analista de métodos y tiempos ha determinado los siguientes tiempos tipo (promedio) en minutos / unidad / operario:
| Operación | Tiempo tipo (promedio) |
| A | 1 minuto |
| B | 6 minutos |
| C | 2 minutos |
| D | 4 minutos |
| E | 2 minutos |
El proceso inicialmente se lleva a cabo con un operario por cada operación. La jornada laboral es de 8 horas por turno, y el salario diario corresponde a $25 USD.
El jefe de planta considera que a simple vista la línea se encuentra desbalanceada. La directiva les exige una producción superior a 230 unidades por turno; para ello le permite disponer de hasta 3 operarios adicionales. Por esta razón utiliza una herramienta de Balanceo de líneas para este fin.
Al utilizar la herramienta de Balance de líneas, obtiene los siguientes resultados:
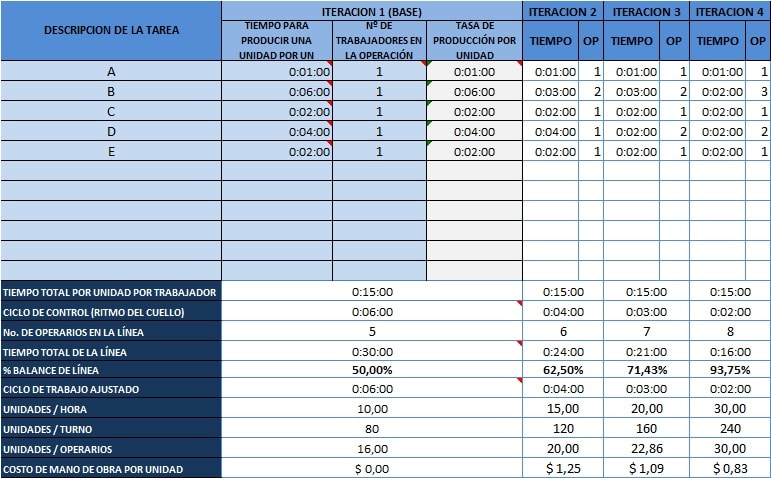
En síntesis, la herramienta le sugiere emplear los 3 operarios adicionales de la siguiente manera: 2 empleados + en la operación B y 1 empleado más en la operación D. Esto, de acuerdo a la herramienta elevaría el proceso hasta obtener una producción de 240 unidades por turno. Sin embargo, algo despierta una duda en el jefe de planta. De acuerdo a la misma herramienta, su producción actual estaría por el orden de las 80 unidades por turno; la verdad: ¡Nunca han alcanzado dicha producción!
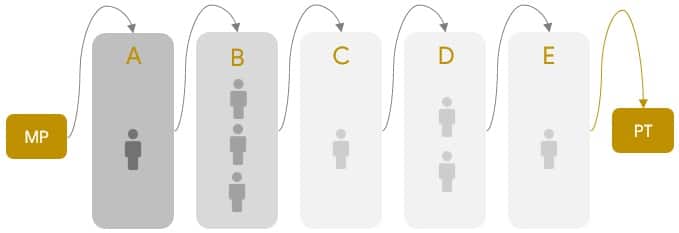
Antes de implementar la solución sugerida en la planta, el jefe de planta prefiere evaluar dicha configuración por medio de simulación. Quiere estar seguro que la herramienta de Balance arroje información confiable. Para este fin utiliza Bizagi, un modelador de procesos. Modelará el proceso inicial, y modelará la configuración de acuerdo al Balance de líneas para un turno de trabajo (8 horas):
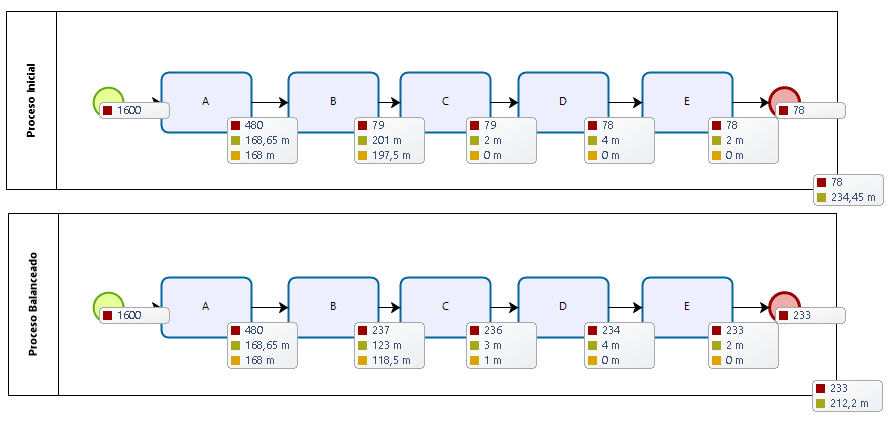
Los resultados de la simulación permiten validar los resultados arrojados por la herramienta de Balance de líneas. En teoría, el proceso pasaría de producir 78 unidades por turno a 233 unidades por turno. Los rendimientos locales se detallan a continuación:
| Operación | Proceso inicial | Proceso balanceado |
| A | 100,00% | 100,00% |
| B | 99,79% | 99,58% |
| C | 32,92% | 98,58% |
| D | 65,62% | 99,54% |
| E | 32,50% | 97,92% |
En materia de costos:
- Costo unitario (Proceso base): 1,60 USD / Unidad
- Costo unitario (Proceso balanceado): 0,86 USD / Unidad
Todo parece indicar que ha considerado todas las variables, dos métodos distintos validan los cálculos. Sin embargo, parece recordar algo: la variabilidad. Ha olvidado considerar la variabilidad en sus cálculos, de manera que contacta al analista de tiempos y le solicita que sustente los tiempos tipo de cada operación.
El analista responde de acuerdo al método utilizado. Por cada operación ha efectuado 50 observaciones, y los tiempos utilizados en todos los cálculos del jefe de planta, son producto de la media de cada conjunto de observaciones. El listado de tiempos es el siguiente:
| Tiempos en minutos | |||||
| Observación | A | B | C | D | E |
| 1 | 0,833 | 5,755 | 2,174 | 4,066 | 2,089 |
| 2 | 0,694 | 5,176 | 2,050 | 3,675 | 1,782 |
| 3 | 1,004 | 6,362 | 2,294 | 4,462 | 2,452 |
| 4 | 0,480 | 3,979 | 1,750 | 2,804 | 1,280 |
| 5 | 0,908 | 6,030 | 2,230 | 4,248 | 2,249 |
| 6 | 0,597 | 4,704 | 1,941 | 3,344 | 1,561 |
| 7 | 0,489 | 4,047 | 1,770 | 2,857 | 1,303 |
| 8 | 1,917 | 8,783 | 2,711 | 5,938 | 4,264 |
| 9 | 0,681 | 5,121 | 2,038 | 3,637 | 1,755 |
| 10 | 0,820 | 5,704 | 2,164 | 4,033 | 2,061 |
| 11 | 1,371 | 7,455 | 2,493 | 5,146 | 3,201 |
| 12 | 0,662 | 5,028 | 2,017 | 3,573 | 1,710 |
| 13 | 0,464 | 3,849 | 1,712 | 2,702 | 1,238 |
| 14 | 1,108 | 6,696 | 2,357 | 4,675 | 2,668 |
| 15 | 0,486 | 4,024 | 1,763 | 2,839 | 1,295 |
| 16 | 0,916 | 6,060 | 2,236 | 4,267 | 2,266 |
| 17 | 0,650 | 4,973 | 2,004 | 3,535 | 1,684 |
| 18 | 0,855 | 5,838 | 2,191 | 4,122 | 2,137 |
| 19 | 1,437 | 7,630 | 2,523 | 5,252 | 3,332 |
| 20 | 1,021 | 6,417 | 2,305 | 4,497 | 2,487 |
| 21 | 1,093 | 6,648 | 2,348 | 4,644 | 2,636 |
| 22 | 0,472 | 3,918 | 1,733 | 2,757 | 1,260 |
| 23 | 0,954 | 6,191 | 2,261 | 4,352 | 2,346 |
| 24 | 1,331 | 7,344 | 2,474 | 5,078 | 3,120 |
| 25 | 1,143 | 6,801 | 2,377 | 4,741 | 2,738 |
| 26 | 1,045 | 6,495 | 2,320 | 4,547 | 2,536 |
| 27 | 0,859 | 5,851 | 2,194 | 4,130 | 2,144 |
| 28 | 0,679 | 5,108 | 2,035 | 3,629 | 1,748 |
| 29 | 1,076 | 6,593 | 2,338 | 4,610 | 2,600 |
| 30 | 0,921 | 6,076 | 2,239 | 4,278 | 2,276 |
| 31 | 2,372 | 9,735 | 2,856 | 6,485 | 5,122 |
| 32 | 1,068 | 6,570 | 2,334 | 4,595 | 2,585 |
| 33 | 0,666 | 5,048 | 2,021 | 3,587 | 1,719 |
| 34 | 0,556 | 4,474 | 1,884 | 3,177 | 1,464 |
| 35 | 0,441 | 3,652 | 1,651 | 2,543 | 1,179 |
| 36 | 0,520 | 4,254 | 1,827 | 3,014 | 1,378 |
| 37 | 0,455 | 3,780 | 1,692 | 2,647 | 1,217 |
| 38 | 0,584 | 4,635 | 1,924 | 3,294 | 1,531 |
| 39 | 2,412 | 9,813 | 2,868 | 6,529 | 5,195 |
| 40 | 0,660 | 5,020 | 2,015 | 3,568 | 1,706 |
| 41 | 0,466 | 3,868 | 1,718 | 2,717 | 1,244 |
| 42 | 0,421 | 3,444 | 1,582 | 2,370 | 1,124 |
| 43 | 0,609 | 4,767 | 1,956 | 3,389 | 1,589 |
| 44 | 0,961 | 6,215 | 2,266 | 4,368 | 2,360 |
| 45 | 0,559 | 4,495 | 1,889 | 3,192 | 1,473 |
| 46 | 2,646 | 10,260 | 2,933 | 6,781 | 5,627 |
| 47 | 3,147 | 11,154 | 3,059 | 7,276 | 6,538 |
| 48 | 0,547 | 4,426 | 1,872 | 3,142 | 1,445 |
| 49 | 0,604 | 4,744 | 1,950 | 3,372 | 1,579 |
| 50 | 0,525 | 4,288 | 1,836 | 3,039 | 1,391 |
| Media descriptiva | 0,944 | 5,786 | 2,144 | 4,030 | 2,274 |
| Redondeo (Minutos) | 1 | 6 | 2 | 4 | 2 |
De acuerdo al listado de tiempos el jefe de planta saca la primera conjetura: pocas veces cada operación toma el tiempo de la media: variabilidad. ¿Cómo ajustar su modelo de acuerdo a la variabilidad? Recordó sus clases de estadística: mediante la distribución de probabilidad de cada operación.
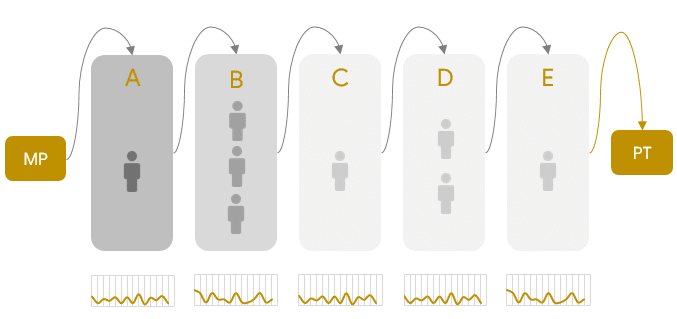
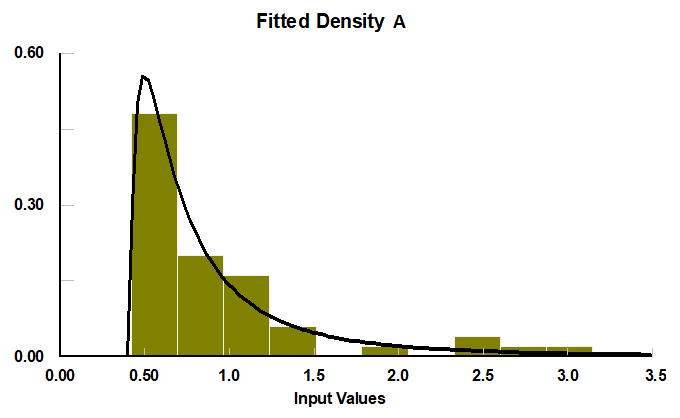
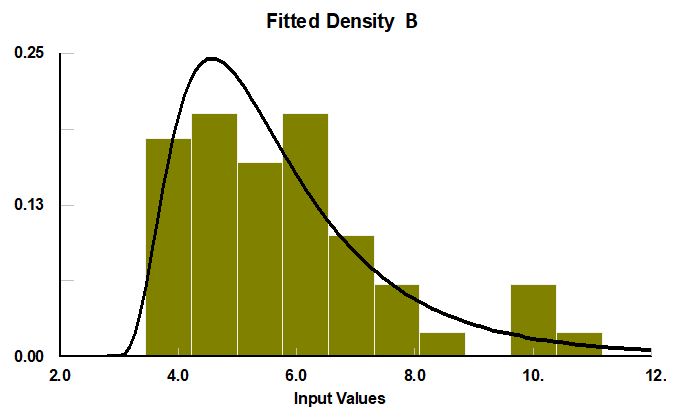
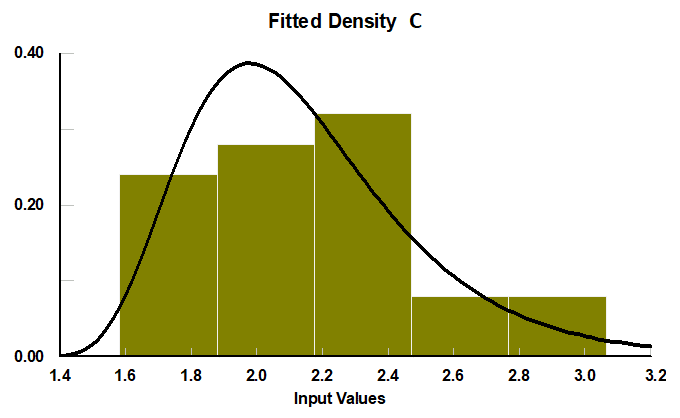
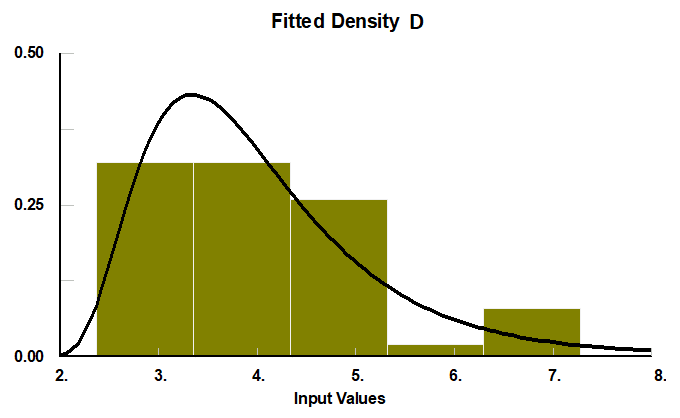
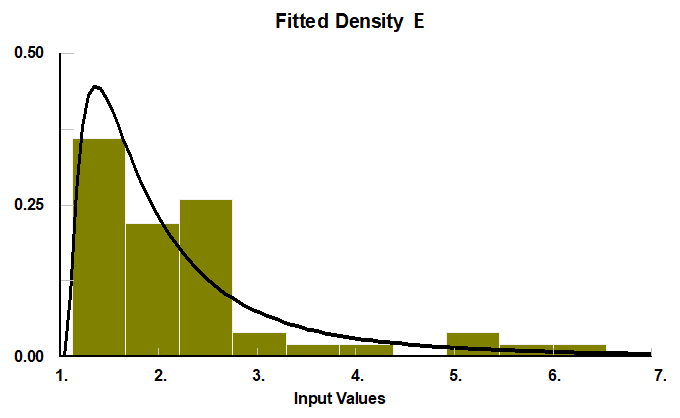
Hallar la distribución de probabilidad de un listado de datos es tarea sencilla si se cuenta con un paquete estadístico, por ejemplo: Stat::fit. Vamos a procesar los datos de las operaciones:
Así se ve la variabilidad.
De acuerdo al procesamiento de todos los datos, tenemos los siguientes resultados:
| Operación | Distribución | Media (D. Normal) | Desviación estándar |
| A | Lognormal | 0,97 | 0,838 |
| B | Lognormal | 5,81 | 1,95 |
| C | Lognormal | 2,14 | 0,357 |
| D | Lognormal | 4,04 | 1,21 |
| E | Lognormal | 3,06 | 3,21 |
Con esta información es posible afectar el modelo de acuerdo a las distribuciones de probabilidad de cada operación. Al correr la simulación (determinística vs. estocástica) tendremos los siguientes resultados:
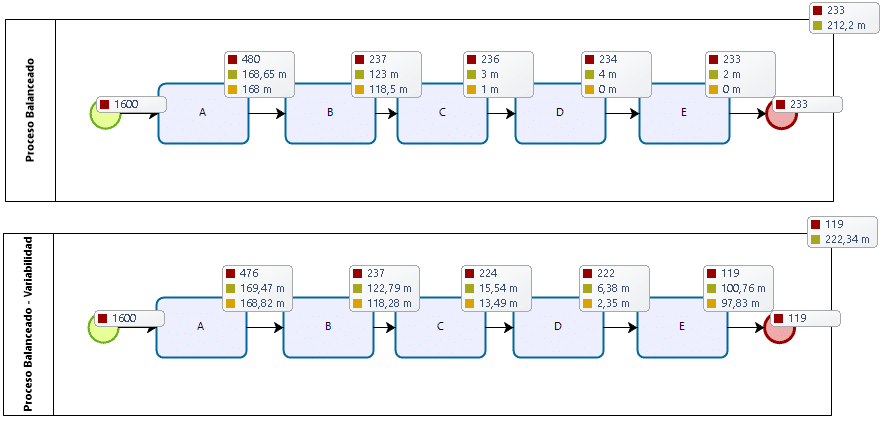
Los resultados de la simulación permiten contrastar los resultados previos con la consideración de la variabilidad. De las 233 unidades / turno teóricas (según el balanceo determinístico); ahora estimamos 119 unidades / turno: Los efectos de la variabilidad . Esto es aproximadamente un 49% menos de lo previsto mediante Balance de líneas. Los rendimientos locales se detallan a continuación:
| Operación | Proceso balanceado | Proceso balanceado – Variabilidad |
| A | 100,00% | 100,00% |
| B | 99,58% | 99,77% |
| C | 98,54% | 98,55% |
| D | 97,92% | 92,98% |
| E | 97,29% | 97,59% |
En materia de costos de mano de obra:
- Costo unitario (Proceso balanceado- determinístico): 0,86 USD / Unidad
- Costo unitario (Proceso balanceado – estocástico): 1,68 USD / Unidad
Imagínese por un momento lo que hubiese podido pasar, si como jefe de planta los estimados de costo se hubiesen establecido de acuerdo al costo unitario de la herramienta de Balance de línea. Esto siembra, del mismo modo, un manto de duda acerca de la pertinencia del tiempo estándar para estimaciones de capacidad / tiempos de entrega y costos de producción.
Es interesante revisar el proceso original (sin balance) afectado por la variabilidad. Veamos la simulación y la comparación:
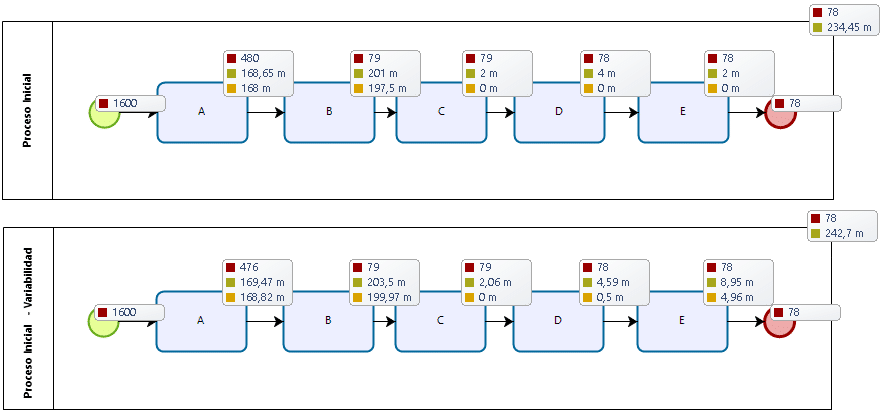
¿Sorpresa? Al parecer, en este caso, la variabilidad no afecta la producción de la línea desbalanceada. Por lo tanto, su costo de mano de obra equivale a:
- Costo unitario (Proceso base – variabilidad): 1,60 USD / Unidad
Sin considerar otros costos, la inclusión de 3 operarios adicionales en la línea no representa una disminución del costo unitario (mano de obra), por el contrario, empeoró su desempeño, aumentó su costo unitario. ¿Existen costos adicionales asociados a aumentar la cantidad inicial de operarios? Seguramente: Equipos, herramientas, redistribución / layout y más variabilidad.
Si desea profundizar acerca de este tema, lo invitamos a leer: Refutación al balanceo de líneas.





Muchas gracias por este artículo.
Finalmente, si agregamos capacidad extra a los C, D y E, incrementaremos el costo total, pero preveo que la producción total subiría al promedio de B, es decir alrededor de 230 por turno. Y esto llevaría a un costo unitario cercano a 1.2, lo que es 25% menos que el original. Es decir, la variabilidad OBLIGA a tener amortiguadores que la absorban. En Teoría de Restricciones hemos desarrollado este conocimiento hace ya décadas. De paso, al lograr esa reducción de costo unitario y lograr la producción requerida, el OEE de cada centro A, C, D y E se redujo a niveles «preocupantes», lo que es lo esperado para maximizar la productividad… Tal vez sea bueno un artículo sobre OEE y cómo es una trampa para la productivdad.
Gracias por tu comentario Matías, y por tu colaboración en el desarrollo del artículo. Esperemos desde luego esa entrada acerca del OEE y su relación con la productividad desde la perspectiva TOC.
Muchas gracias por el artículo, es bastante interesantes y la vez sorprendente.
Por otra parte, tengo una consulta. ¿ Por qué existe resultados diferentes cuando se usa el programa BizAgi, ya que al hacer la simulación nos da un resultado de 78 unidades y cuando se hace el cálculo mediante Excel nos da 80 unidades (proceso sin balancear)? incluso cuando se hace el balanceo y se prueba una simulación en BizAgi nos da un resultado de 233 mientras que en Excel 240 unidades. ¿ A qué se debe esas diferencias o cual de ellas se debe considerar y por qué?
Hola Kenyi, gracias por tus comentarios. La verdad, creería que esa pequeña diferencia puede guardar relación con el tiempo que se toma cada proceso en iniciar la operación sobre la primera unidad del lote. Ya que Bizagi simula una secuencia, este tiempo es considerado, a diferencia del modelo de Excel.
Hola, tengo una consulta. ¿Cómo obtuvo los resultados para el ajuste de la variabilidad mediante el uso del programa Stat::fit.,? ya que ingresé los datos al programa mencionado pero no logré obtener los mismo resultados con respecto a la media con distribución Lognormal. Por favor, si pudiera explicar brevemente los pasos del programa para obtener los mismos resultados presente en el cuadro.
Muchas gracias por compartir sus conocimientos.
Hola, tengo una consulta. Al momento de ingresar los mismos datos mencionados en el programa Stat::fit del ejemplo con distribución Lognormal no logré obtener los mismos resultados del cuadro con respecto a la media (0.97, 5.81, 2.14, 4.04, 3.06). Podría por favor nombrar los pasos para llegar a tener los mismos resultados del cuadro mencionado en el programa Stat::fit,?
Muchas gracias por compartir su conocimiento.