La secuenciación tiene distintos niveles de complejidad, ya veíamos como se aplicaban principios de prioridad para elegir el mejor orden para procesar distintas operaciones que pasaban por un centro de trabajo; el siguiente nivel corresponde en determinar la secuencia para efectuar el mismo proceso pero esta vez para dos centros de trabajo.
En la industria, y por muchos años la regla de Johnson se ha aplicado con gran éxito para minimizar el tiempo de procesamiento global.
¿En qué consiste la Regla de Johnson?
La regla de Johnson es un algoritmo heurístico utilizado para resolver situaciones de secuenciación de procesos que operan dos o más órdenes (operaciones) que pasan a través de dos máquinas o centros de trabajo. Su principal objetivo es minimizar el tiempo de procesamiento total del grupo de trabajos. Este algoritmo consiste en la aplicación de cuatro sencillos pasos:
El primer paso consiste en listar todos los trabajos u operaciones junto con su tiempo de procesamiento por cada centro de trabajo o máquina.
El segundo paso consiste en seleccionar el tiempo de procesamiento más corto. Recuerde que como resultado de la aplicación del paso 1 obtenemos dos columnas de tiempos (tiempos del centro de trabajo 1 y 2); Sí el tiempo más corto se encuentra en la columna correspondiente al centro de trabajo (máquina) 1, este trabajo se programa primero, en caso contrario y de estar en la columna correspondiente al centro de trabajo 2, este trabajo se programa al final. Cualquier empate puede romperse de forma arbitraria.
Una vez se programa un trabajo, sea al inicio o sea al final, este se elimina de la lista inicial.
Se deben repetir los pasos 2 y 3 para los trabajos restantes, trabajando hacia el centro de la secuencia.
Ejemplo de la aplicación de la Regla de Johnson
El taller de metalmecánica «Abelito» tiene para su programación 5 órdenes de trabajo; se trata de piezas de acero inoxidable de geometrías distintas, para ello la materia prima (bloques de acero inoxidable) debe ser primero torneada, según especificaciones particulares de cada pieza; luego son pasadas al centro de fresado, en el cual adquieren geometrías diversas según las precisiones del plano que la acompañan.
El orden de trabajo no es conmutativo, por lo cual es imperativo que antes de que cada pieza sea fresada deberá haber pasado por el proceso de torneado. Los tiempos de torneado y fresado de cada pieza se especificarán en el siguiente tabulado:
| Orden | Torneado (horas) | Fresado (horas) |
| Pieza A | 1,2 | 1,8 |
| Pieza B | 2,2 | 0,8 |
| Pieza C | 0,7 | 3,1 |
| Pieza D | 0,5 | 1,1 |
| Pieza E | 1,5 | 2,3 |
Con base en lo anterior, debemos efectuar una secuenciación que minimice el tiempo total de programación, para ello utilizaremos la regla de Johnson.
Solución
El primer paso consiste entonces en listar los trabajos junto a sus respectivos tiempos de procesamiento en los centros de trabajo, para lo cual hacemos uso del tabulado del enunciado del problema:
| Orden | Torneado (horas) | Fresado (horas) |
| Pieza A | 1,2 | 1,8 |
| Pieza B | 2,2 | 0,8 |
| Pieza C | 0,7 | 3,1 |
| Pieza D | 0,5 | 1,1 |
| Pieza E | 1,5 | 2,3 |
El segundo paso consiste en seleccionar el tiempo de procesamiento más corto, como este se encuentra en el centro de trabajo 1 (torneado, primera columna), se programa de primero:
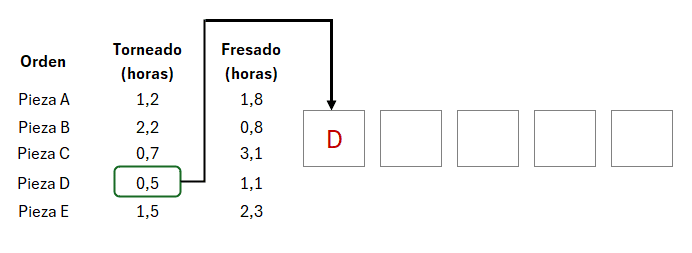
El tercer paso consiste en eliminar de la lista la orden que fue asignada:
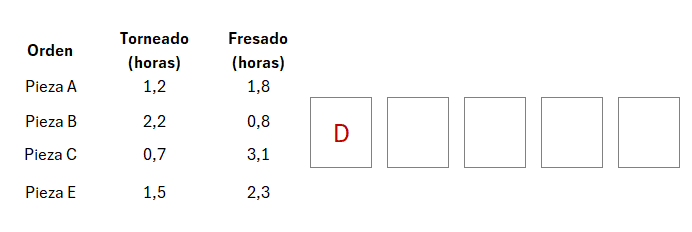
El último paso indica la repetición de los pasos 2 y 3 hasta asignar la totalidad de órdenes:
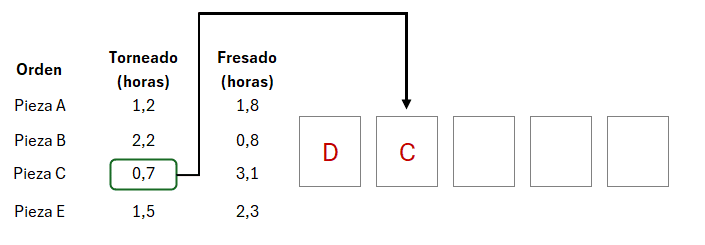
En la asignación del orden del siguiente trabajo podemos observar que el tiempo menor se encuentra en la segunda columna, correspondiente al proceso de fresado, razón por la cual este trabajo se programará de último:
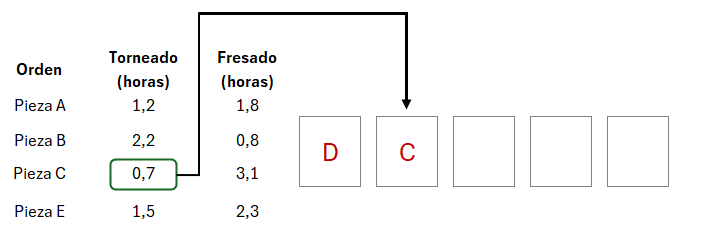
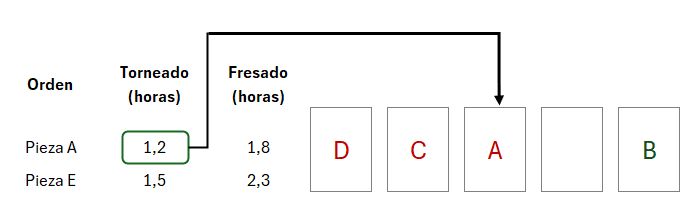
El último trabajo se asignará por lógica en el orden que queda disponible, por lo cual la secuencia obtenida mediante la aplicación de la regla de Johnson es la siguiente:

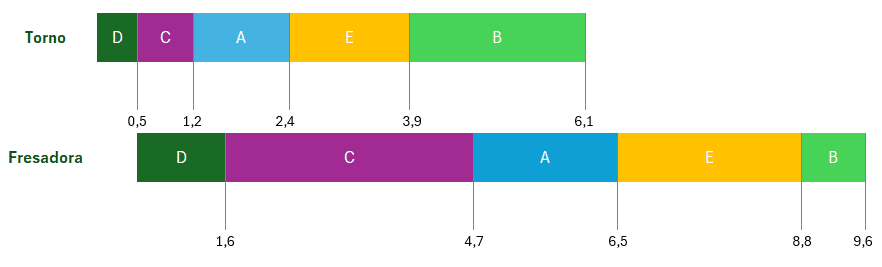
Podemos observar como el centro de fresado debe esperar 0,5 horas para recibir la pieza D proveniente del centro de torneado; además, podemos observar como el tiempo total de programación es igual a 9,6 horas.





Estimado, ¿el metodo de Johnson puede ser considerado como una heuristica golosa/voraz?
Podría inferirse, dado que en la regla de Johnson, la heurística consiste en elegir el tiempo de procesamiento más corto en cada paso (solución óptima).
Que softwares o aplicaciones utilizan para hacer sus graficos??
¿Funciona para màs maquinas?
Ejemplo necesito ordenar n numero de productos en 19 màquinas
No funciona, maximo para 3 maquinas segun lo que he visto, para lo que tu quieres ya se debe usar progrmacion lineal y minimizar makesapan
Interesante los materiales , gracias
No funciona, maximo para 3 maquinas segun lo que he visto, para lo que tu quieres ya se debe usar progrmacion lineal y minimizar makesapan
Atractiva la Información