El método de la esquina Noroeste es un algoritmo heurístico capaz de solucionar problemas de transporte o distribución, mediante la consecución de una solución básica inicial que satisfaga todas las restricciones existentes, sin que esto implique que se alcance el costo óptimo total.
Este método tiene como ventaja frente a sus similares, la rapidez de su ejecución, y es utilizado con mayor frecuencia en ejercicios donde el número de fuentes y destinos sea muy elevado.
Su nombre se debe al génesis del algoritmo, el cual inicia en la ruta, celda o esquina Noroeste. Es común encontrar gran variedad de métodos que se basen en la misma metodología de la esquina Noroeste, dado que podemos encontrar de igual manera el método e la esquina Noreste, Sureste o Suroeste.
Algoritmo de resolución de la Esquina Noroeste
Se parte por esbozar en forma matricial el problema, es decir, filas que representen fuentes y columnas que representen destinos, luego el algoritmo debe de iniciar en la celda, ruta o esquina Noroeste de la tabla (esquina superior izquierda).
En la celda seleccionada como esquina Noroeste se debe asignar la máxima cantidad de unidades posibles, cantidad que se ve restringida ya sea por las restricciones de oferta o de demanda. En este mismo paso se procede a ajustar la oferta y demanda de la fila y columna afectada, restándole la cantidad asignada a la celda.
Paso 2
En este paso se procede a eliminar la fila o destino cuya oferta o demanda sea 0 después del «Paso 1», si dado el caso ambas son cero arbitrariamente se elige cual eliminar y la restante se deja con demanda u oferta cero (0) según sea el caso.
Paso 3
Una vez en este paso existen dos posibilidades, la primera que quede un solo renglón o columna, si este es el caso se ha llegado al final el método, «detenerse».
La segunda es que quede más de un renglón o columna, si este es el caso iniciar nuevamente el «Paso 1».
Ejemplo del Método de la Esquina Noroeste
Por medio de este método resolveremos el problema de transporte propuesto y resuelto en artículos anteriores mediante programación lineal.
Una empresa energética colombiana dispone de cuatro plantas de generación para satisfacer la demanda diaria eléctrica en cuatro ciudades, Cali, Bogotá, Medellín y Barranquilla. Las plantas 1,2,3 y 4 pueden satisfacer 80, 30, 60 y 45 millones de KW al día respectivamente. Las necesidades de las ciudades de Cali, Bogotá, Medellín y Barranquilla son de 70, 40, 70 y 35 millones de Kw al día respectivamente. Los costos asociados al envío de suministro energético por cada millón de KW entre cada planta y cada ciudad son los registrados en la siguiente tabla.
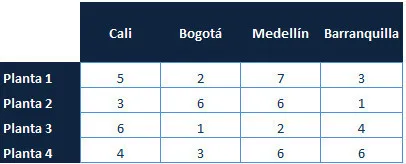
Formule un modelo de programación lineal que permita satisfacer las necesidades de todas las ciudades al tiempo que minimice los costos asociados al transporte.
Solución paso a paso
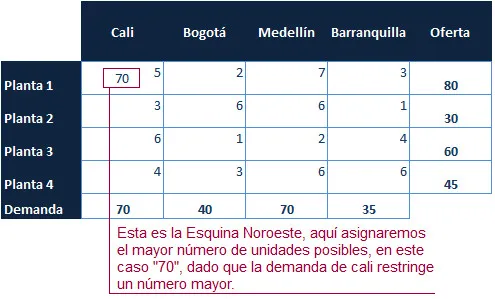
Ahora la cantidad asignada a la esquina noroeste es restada a la demanda de Cali y a la oferta de la «Planta 1», en un procedimiento muy lógico. Dado que la demanda de Cali una vez restada la cantidad asignada es cero (0), se procede a eliminar la columna. El proceso de asignación nuevamente se repite.
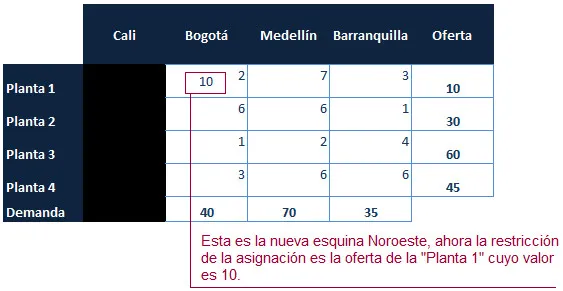
Continuamos con las iteraciones.

En este caso nos encontramos frente a la elección de la fila o columna a eliminar (tachar), sin embargo podemos utilizar un criterio mediante el cual eliminemos la fila o columna que presente los costos más elevados. En este caso la «Planta 2».
Nueva iteración:
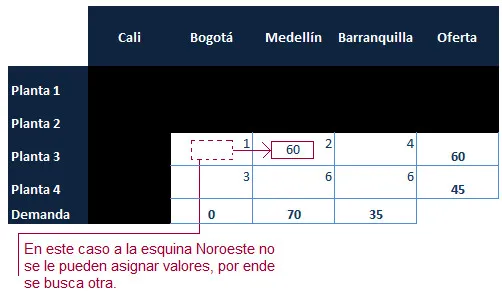
Una vez finalizada esta asignación, se elimina la «Planta 3» que ya ha sido satisfecha con la asignación de 60 unidades, por ende nos queda una sola fila a la cual le asignamos las unidades estrictamente requeridas y hemos finalizado el método.
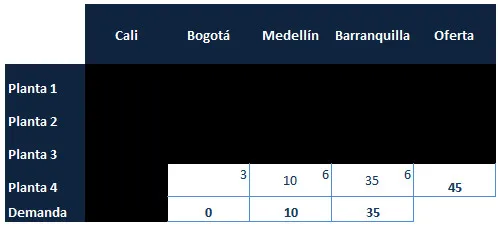
El cuadro de las asignaciones (que debemos desarrollarlo paralelamente) queda así:
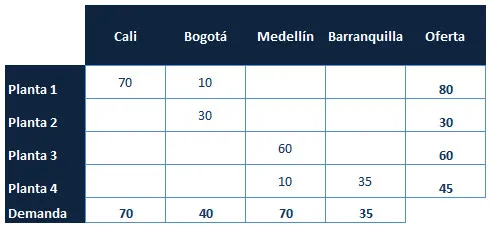
Los costos asociados a la distribución son:
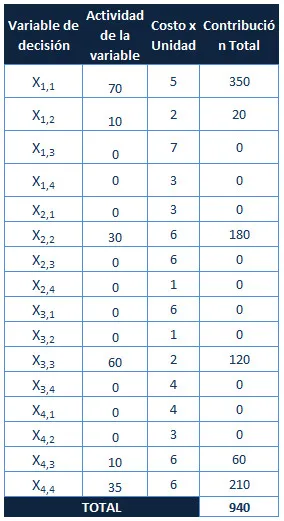
El costo total es evidentemente superior al obtenido mediante Programación Lineal y el Método de Aproximación de Vogel, lo cual demuestra lo enunciado en la descripción del algoritmo que cita que no obtiene siempre la mejor solución, sin embargo presenta un cumplimiento de todas las restricciones y una rapidez de elaboración, lo cual es una ventaja en problemas con innumerables fuentes y destinos en los cuales no nos importe más que satisfacer las restricciones.





MUY ÚTIL, GRACIAS POR SUBIR ESTOS CONTENIDOS
de donde saco el costo de envio?, me podrias explicar
Sonia, un saludo. Los costos de envío son dados por el problema.
Buenas tardes, es necesario explicar los costos asociados de distribución?
Hola Robert. En la práctica es preferible, dado que las variables de decisión estás ligadas a un peso dentro de la función objetivo, que generalmente es el costo. Recomendaría siempre detallar los costos asociados a la distribución.
si el problema no tubiera sumatoria al final para sacar el costo como le haria
Que pasa si la oferta y demanda al inicio son 70 y 70 cual selecciono ?
si mis costos tuviesen una M no se podría asignar ahí y me tocaría rodarme a la siguiente columna o si se asigna. Es decir, como esquina noroeste no tiene en cuenta los costos, lo asignaria segun la regla normalmente?
Hola, Que se hace cuando el problema te da costos M?
Yo tengo una pregunta, qué pasa si al final no me cuadra, y me queda una cantidad todavía, tengo que volver a empezar?
Yo tengo una pregunta, qué pasa si al final no me cuadra, y me queda una cantidad todavía, tengo que volver a empezar el cuadro?
pones un destino o un centro de distribución ficticio
Muy Util el contenido