La mejor forma de llevar el juego es a través de una visita guiada, en la cual te mostraremos diversas configuraciones para comprender algunos conceptos a través de los escenarios del juego.
Juego 1: ¡Línea sin variabilidad!
Antes que nada, podemos mencionar que este es el escenario que nos plantea el Balance de Líneas convencional, es decir, una línea interdependiente (el proceso A pasa unidades a B, el proceso B pasa unidades a C, y así sucesivamente de forma secuencial), pensada como ajena a la incertidumbre, donde la capacidad de producción es conocida e inalterable, es decir: ¡invariable!
Configuremos una simulación de 20 rondas (ciclos de producción), y lo más importante, ajustemos la capacidad de cada una de las estaciones de la línea de producción de pizzas. En cada estación encontraremos un deslizador para configurar la capacidad mínima y máxima de procesamiento (valor mínimo del dado y valor máximo del dado). En este escenario en el que no existe variabilidad, la capacidad mínima es igual a la capacidad máxima, es decir, es exacta: ¡invariable! Por un momento piense en la posibilidad de lanzar un dado y que siempre, invariablemente salga el mismo valor.
Como sugerencia, ubique la capacidad en el valor de 4, es decir, cada una de las estaciones tiene la capacidad de procesar y enviar 4 pizzas (en proceso) a la estación siguiente (el dado siempre caerá en el valor de 4).
El WIP inicial, que corresponde al inventario previo de cada estación, lo podemos dejar en 4 unidades, para que podamos tener producto terminado desde el primer ciclo, sin la necesidad de que las estaciones finales esperen que se realice el primer lote que involucre a todas las operaciones de la línea (setup).
En este primer escenario podemos dejar el WIP máximo en 100 (excesivo) de manera predeterminada.
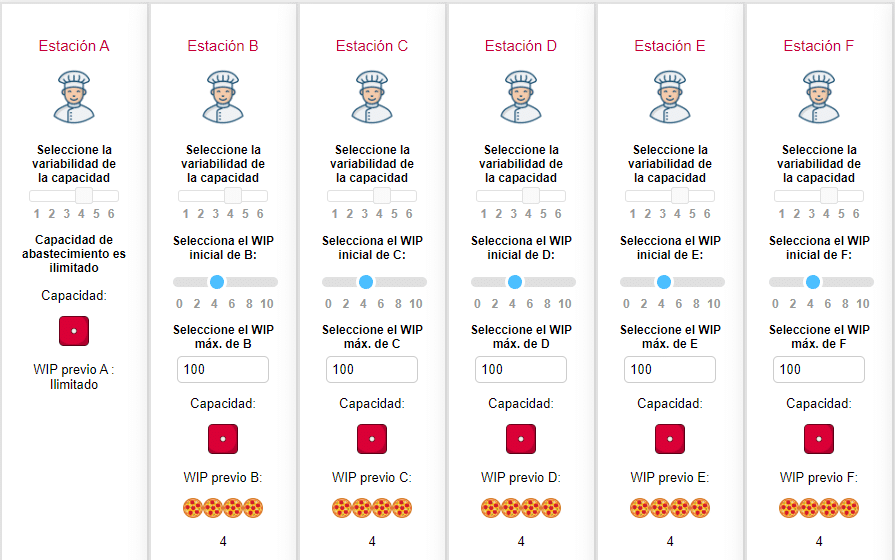
Podemos iniciar la simulación y ver cada una de las rondas: ¡Lanzamiento de dados! >> ¡Movimiento de piezas!, pero encontraremos que no pasa nada fuera de lo común, ya que no existe variabilidad, el flujo es «perfecto»: la tasa de producción es fija y constante, además no existe acumulación de inventario en el sistema (salvo las mismas unidades establecidas como WIP inicial). Podemos acelerar la simulación en cualquier momento.
| Mínima capacidad media de las estaciones | 4 pizzas |
| Producción estimada de acuerdo a la estación restricción | 80 pizzas |
| Producción simulada con variabilidad (Throughput) | 80 pizzas |
| Tasa producción real / estimada por capacidad mínima | 100% |
| WIP total inicial | 20 pizzas |
| WIP total final | 20 pizzas |
En el caso en que simulemos que cada ronda es una hora de operación, podemos utilizar los mismos datos de entrada para simular el comportamiento de la línea mediante nuestro aplicativo de balance de líneas (6 estaciones, los tiempos de procesamiento serían de 15 minutos / pizza, tendríamos 1 operario por estación y 1200 minutos por turno). Los resultados serían:
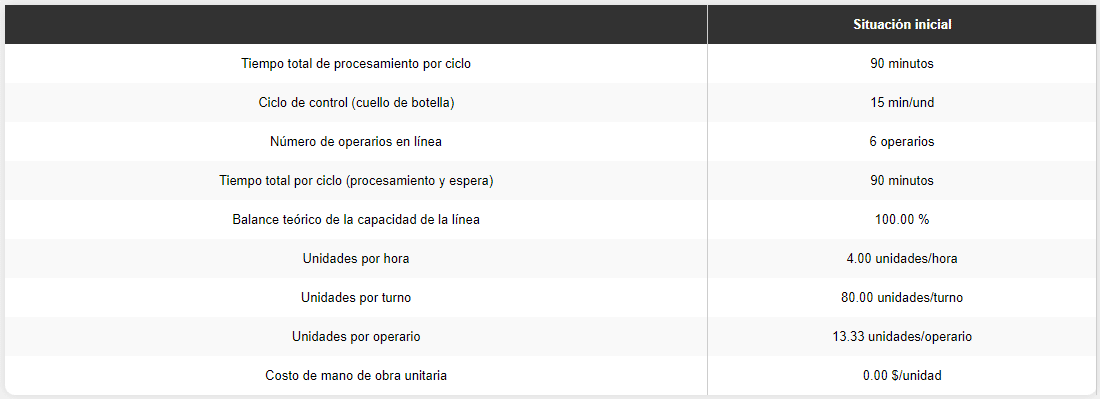
En términos generales, al no considerar la variabilidad, obtuvimos los resultados que estimaría un Balanceo de Líneas Convencional. Esto nos lleva a pensar que muchas de las herramientas que nos enseñan en programas académicos están concebidas sobre la base de supuestos que rara vez tienen una apliación práctica.
Juego 2: ¡Tenemos variabilidad!
En este escenario de simulación planteamos la posibilidad de considerar las fluctuaciones estadísticas asociadas al lanzamiento de un dado, no es un contexto abstracto para nosotros. Consideraremos todo el rango de opciones, de manera que la capacidad de cada estación en cada ronda estará determinada por un número aleatorio entre 1 y 6 (las caras de un dado).
¿Qué herramientas nos dan en la universidad para estimar la producción asociada a esta línea? Seguramente recordaremos nuestros clases de Estudio de Tiempos, más específicamente cuando determinábamos el tiempo estándar, que es una medida de capacidad media. La metodología del estudio de tiempos nos llevaría a registrar un conjunto de observaciones (lanzamiento del dado), y a calcular un valor medio (capacidad media o tiempo estándar). Si hiciéramos lo mismo con el lanzamiento de un dado, y lo repitiéramos muchas veces, encontraríamos que su lanzamiento medio oscila el valor de 3,5 (a veces más, a veces menos).
Si utilizamos estadística descriptiva tendremos que:
| Media | (1 + 2 + 3 + 4 + 5 + 6) / 6 = 3,5 |
| Mediana | (3 + 4) / 2 = 3,5 |
| Rango | (6 – 1) = 5 |
Lo más probable es que de acuerdo a esta herramientas, consideremos que la capacidad media de cada estación es de 3,5 pizzas por ronda. Así entonces, podemos hacer un cálculo de acuerdo al número de rondas (20 rondas) y proyectar una producción de 70 pizzas al finalizar la simulación.
En este caso vamos a establecer un WIP de 4 pizzas previo a cada estación (0,5 pizzas por encima de la media) y vamos a dejar el WIP máximo de manera predeterminada (excesivo).

Podemos iniciar la simulación y ver cada una de las rondas: ¡Lanzamiento de dados! >> ¡Movimiento de piezas!, en este caso encontraremos, con una alta probabilidad que la capacidad de todas las estaciones no es la misma (variabilidad). Esto genera efectos interesantes y sistémicos. Veamos los resultados de una simulación:
| Mínima capacidad media de las estaciones | 3,5 pizzas |
| Producción estimada de acuerdo a la estación restricción | 70 pizzas |
| Producción simulada con variabilidad (Throughput) | 54 pizzas |
| Tasa producción real / estimada por capacidad mínima | 77,14% |
| WIP total inicial | 20 pizzas |
| WIP total final | 32 pizzas |
*Cada simulación presentará resultados diferentes
En el caso en que simulemos que cada ronda es una hora de operación, podemos utilizar los mismos datos de entrada para simular el comportamiento de la línea mediante nuestro aplicativo de balance de líneas (6 estaciones, los tiempos de procesamiento serían de 17,143 minutos / pizza, tendríamos 1 operario por estación y 1200 minutos por turno). Los resultados serían:
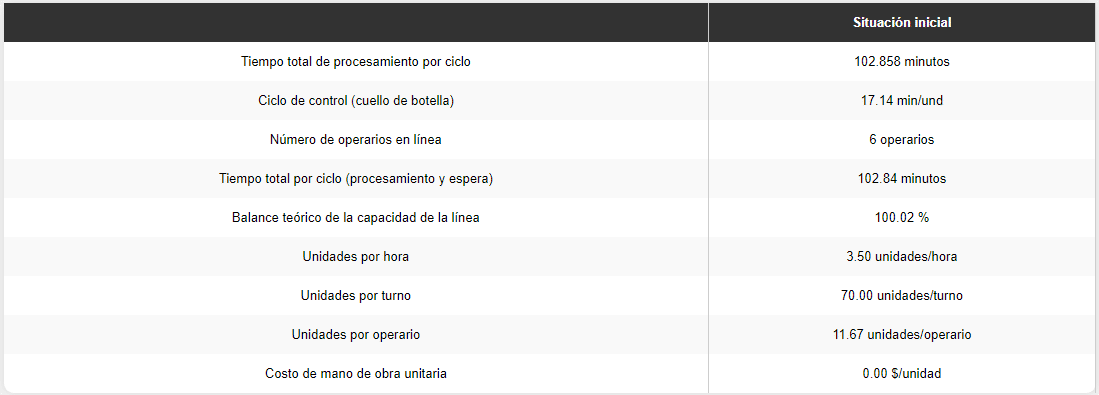
¿Qué pasó? ¿Por qué si existe un perfecto balance entre la capacidad de cada una de las estaciones de la línea (3,5), la producción simulada fue de apenas 54 pizzas tras finalizar las 20 rondas, apenas de un 77,14% respecto a la producción estimada por la capacidad media (70 pizzas)?
Lo que realmente sucedió fue que en la simulación (y en cualquier escenario regido por la variabilidad), lo que ocurre es que las variaciones aleatorias en los lanzamientos determina que las estaciones obtienen una capacidad de procesamiento más alto que el inventario de producto en proceso previo (WIP), mientras otras estaciones obtienen un valor más bajo.
Veamos desde la simplicidad lo que pasaría en ambos escenarios para cada estación:
- Nuestra capacidad de procesamiento es mayor que nuestro WIP previo: Tenemos, por ejemplo, una capacidad de procesar 5 pizzas en una ronda y nuestro WIP (materia prima) es de 2 pizzas. ¿Cuánto podemos realmente procesar? ¡Exacto! 2 pizzas. Y esta producción genera un efecto sobre las operaciones siguientes.
- Nuestra capacidad de procesamiento es menor que nuestro WIP previo: Tenemos, por ejemplo, una capacidad de procesar 2 pizzas en una ronda y nuestro WIP (materia prima) es de 5 pizzas. ¿Cuánto podemos realmente procesar? ¡Exacto! 2 pizzas. Y esta producción genera un efecto sobre las operaciones siguientes.
De tal manera que para que el flujo sea constante y se cumplan las expectativas iniciales, tendría que suceder que cada estación duarante las rondas que dure la simulación, tendría que tener una capacidad de procesamiento y un inventario superior a 3,5. ¡Absolutamente improbable!
Veamos, por ejemplo, el comportamiento de la Estación F:
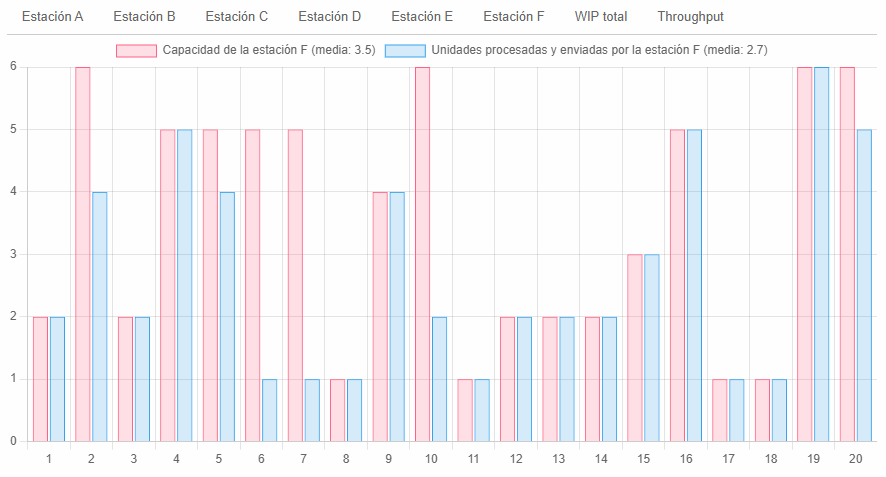
La capacidad media fue exactamente igual a nuestra estimación inicial, coincidiendo con la media descriptiva y con la mediana: 3,5. Sin embargo, su tasa de procesamiento real fue de 2,7 pizzas por ronda, de manera que el sistema tuvo esa tasa de producción. Cuando vemos el gráfico, podemos encontrar rondas como:
| Ronda | Capacidad | Unidades procesadas |
| 2 | 6 | 4 |
| 5 | 5 | 5 |
| 6 | 5 | 1 |
| 7 | 5 | 1 |
| 10 | 6 | 2 |
| 20 | 6 | 5 |
¿Qué rigió el procesamiento real en estas rondas? El desabastecimiento de la estación, es decir, no tener suficiente materia prima para aprovechar su capacidad instalada en cada ronda. Y este desabastecimiento es un efecto sistémico de la desincronización de la línea. Es decir, en una línea regida por la variabilidad, el balance de capacidad es un espejismo.
Si revisamos la capacidad media simulada (para este caso) de cada estación tenemos:
| Estación | Capacidad media simulada | Unidades procesadas |
| A | 3.3 | 3.3 |
| B | 3.45 | 3.2 |
| C | 3.1 | 2.95 |
| D | 3.2 | 2.85 |
| E | 3.2 | 2.85 |
| F | 3.5 | 2.7 |
Varias cosas:
- La capacidad media dimulada de la estación A es igual a su producción media, y la razón es simple, no tiene rotura de WIP debido a que la estación inicial tiene abastecimiento ilimitado.
- La restricción en términos de capacidad media es la Estación C, aun así, no tiene la menor tasa de producción, y la razón es simple, ya que, el efecto de la rotura de WIP se traslada en mayor medida sobre las estaciones siguientes. Ninguna estación posterior podrá tener una tasa de procesamiento superior a la restricción, y la restrición se comienza a expresar en términos de unidades procesadas, ya que determina el WIP de la estación siguiente.
Por último, preste atención al WIP del sistema, ya que al existir diferencia entre la oferta y la demanda enre estaciones se producen ambos fenómenos simultáneamente: ¡Desabastecimiento y acumulación! El WIP del sistema aumentó de un WIP inicial de 20 pizzas en proceso a 32.
Juego 3: ¡Mismo promedio, menor variabilidad!
Ahora vamos a afectar los dados… Digamos que tenemos dados cuyas caras tienen valores que van desde el 3 al 4. Consideraremos todo el rango de opciones, de manera que la capacidad de cada estación en cada ronda estará determinada por un número aleatorio entre 3 y 4 (las caras de un dado).
¿Qué herramientas nos dan en la universidad para estimar la producción asociada a esta línea? Nuevamente el Estudio de Tiempos, más específicamente cuando determinábamos el tiempo estándar, que es una medida de capacidad media. La metodología del estudio de tiempos nos llevaría a registrar un conjunto de observaciones (lanzamiento del dado), y a calcular un valor medio (capacidad media o tiempo estándar). Si hiciéramos lo mismo con el lanzamiento de este particular dado, y lo repitiéramos muchas veces, encontraríamos que su lanzamiento medio oscila el valor de 3,5 (a veces más, a veces menos).
Si utilizamos estadística descriptiva tendremos que:
| Media | (3 + 4) / 2 = 3,5 |
| Mediana | (3 + 4) / 2 = 3,5 |
| Rango | (4 – 3) = 1 |
Lo más probable es que de acuerdo a esta herramientas, consideremos que la capacidad media de cada estación es de 3,5 pizzas por ronda. Así entonces, podemos hacer un cálculo de acuerdo al número de rondas (20 rondas) y proyectar una producción de 70 pizzas al finalizar la simulación. Pero, ¡Un momento! Acabamos de simular la producción de una línea idéntica con capacidad balanceada de media 3,5 pizzas por ronda. ¿Acaso los resultados no deberían ser los mismos?
En este caso vamos a establecer un WIP de 4 pizzas previo a cada estación (0,5 pizzas por encima de la media) y vamos a dejar el WIP máximo de manera predeterminada (excesivo).
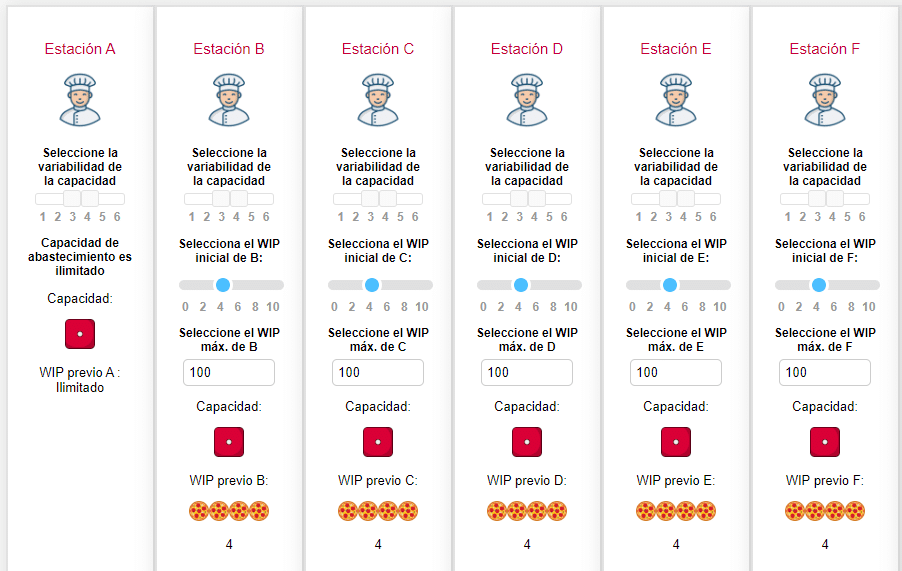
Veamos los resultados de una simulación en particular:
| Mínima capacidad media de las estaciones | 3,5 pizzas |
| Producción estimada de acuerdo a la estación restricción | 70 pizzas |
| Producción simulada con variabilidad (Throughput) | 66 pizzas |
| Tasa producción real / estimada por capacidad mínima | 94,29 % |
| WIP total inicial | 20 pizzas |
| WIP total final | 24 pizzas |
*Cada simulación presentará resultados diferentes
¡No hay mucho que agregar! Aun cuando la capacidad media fue igual al escenario anterior, una disminución en la variabilidad de todos los procesos, mejoró sustancialmente el Throughput. Es el momento de que reconsidere si todo ese conjunto de herramientas que le enseñaron en la universidad bajo el supuesto de «no considera la variabilidad» tiene un efecto práctico.
Juego 4: ¡Mismo promedio, diferente variabilidad entre estaciones! ¡Una restricción!
Pensemos por un segundo en si la variabilidad, en un contexto de aplicación real, afecta de la misma manera y en la misma proporción a todas las operaciones que hacen parte de una línea interdependieente. Pues bien, eso es lo que vamos a considerar: Todas las estaciones tendrán la misma capacidad media: 3,5 pizzas por estación, y todas, excepto la estación B, tendrán una baja variabilidad (entre 3 y 4 pizzas por ronda), mientras la estación B tendrá una variabilidad alta (entre 1 y 6 pizzas) por ronda.
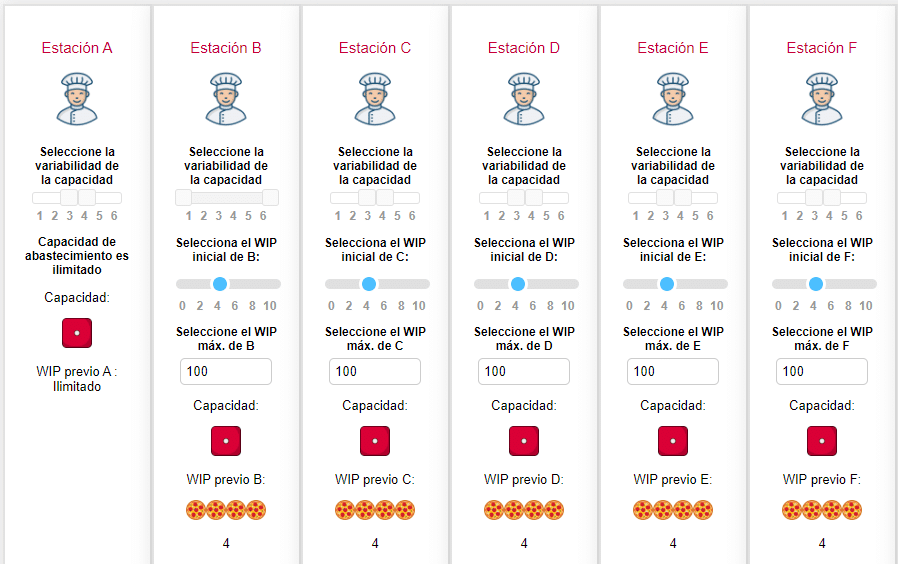
Veamos los resultados de una simulación en particular:
| Mínima capacidad media de las estaciones | 3,5 pizzas |
| Producción estimada de acuerdo a la estación restricción | 70 pizzas |
| Producción simulada con variabilidad (Throughput) | 58 pizzas |
| Tasa producción real / estimada por capacidad mínima | 82,86 % |
| WIP total inicial | 20 pizzas |
| WIP total final | 30 pizzas |
*Cada simulación presentará resultados diferentes
La imagen final de esta simulación es la siguiente:

El solo hecho de aumentar la variabilidad de una sola estación (B), cuya capacidad media era idéntica al resto de estaciones de la línea interdependiente (línea con capacidad media balanceada), la convirtió en una restricción del sistema.
La restricción o el eslabón más débil del sistema generalmente se puede identificar observando el comportamiento del WIP durante varias rondas. Se esperaría ver una acumulación de pizzas antes de la resttricción, y, quizás, una falta de WIP justo después de él, o por lo menos, una diferencia sustancial entre los WIP’s (antes y después de la restricción). No siempre un WIP grande previo a la restricción implica que esta sea una restricción, ya que puede ser una estación con una gran capacidad de procesamiento.
Si observamos la imagen, hay una diferencia sustancial entre el WIP previo a B y el WIP posterior a B; en este caso, la estación B limitó la productividad de todo el sistema. Veamos algunas cosas especiales.
Si revisamos la capacidad media simulada (para este caso) de cada estación tenemos:
| Estación | Capacidad media simulada | Unidades procesadas |
| A | 3.4 | 3.4 |
| B | 2.85* | 2.75 |
| C | 3.45 | 2.7 |
| D | 3.6 | 2.75 |
| E | 3.5 | 2.75 |
| F | 3.35 | 2.9 |
*Particularmente en esta simulación, la capacidad media de la estación B estuvo muy por debajo de la media descriptiva.
Ahora veamos el efecto que tuvo la restricción sobre la estación siguiente:
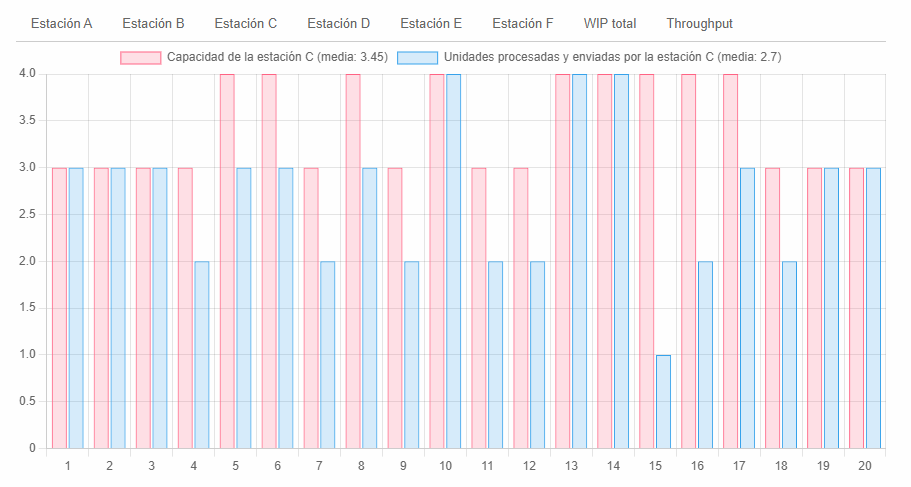
Se pueden observar 12 rondas donde el WIP previo de C (determinado por la producción de B), estuvo por debajo de la capacidad real de la estación C. Esto genera un efecto en cadena sobre las estaciones siguientes, afectando laproductividad del sistema.
Juego 5: ¡Una hora ganada donde no hay una restricción!
Para poner en práctica este concepto vamos a recurrir a una línea desbalanecada (desde su capacidad media), con variabilidad, donde se identifique claramente la restricción:
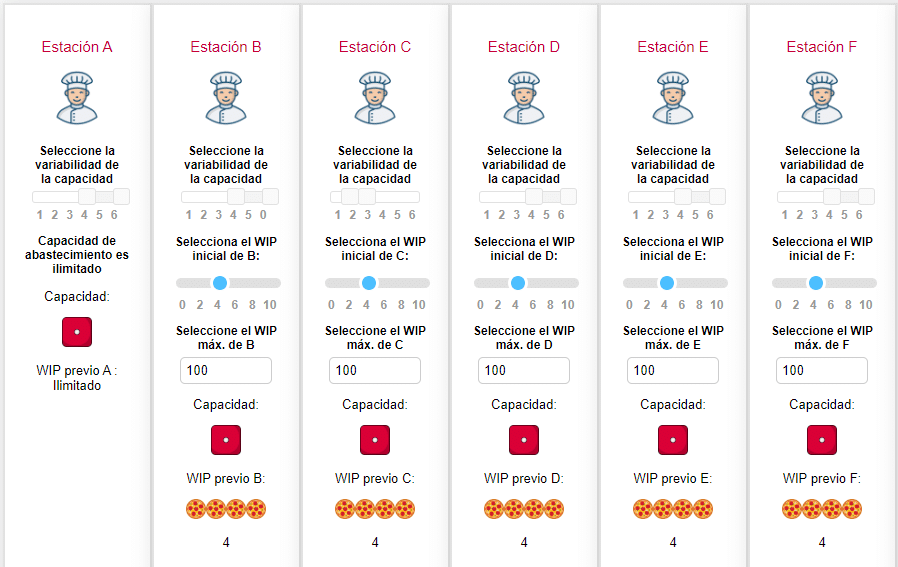
Podemos ver cómo la estación C tiene una menor capacidad de procesamiento que las estaciones restantes (previas y posteriores). Además vemos cómo, se estaría operando sobre la base de aprovechamiento máximo de la capacidad instalada.
Veamos el resultado de una simulación particular:
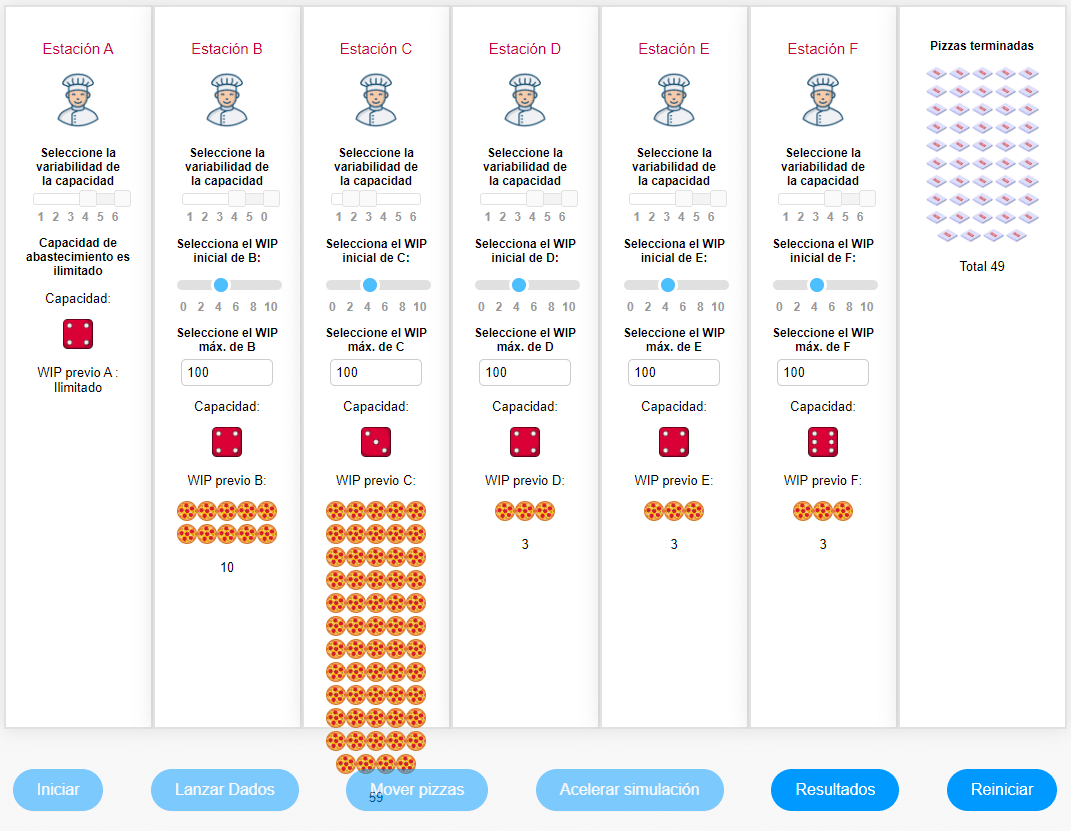
| Mínima capacidad media de las estaciones | 2,5 pizzas |
| Producción estimada de acuerdo a la estación restricción | 50 pizzas |
| Producción simulada con variabilidad (Throughput) | 49 pizzas |
| Tasa producción real / estimada por capacidad mínima | 98,00 % |
| WIP total inicial | 20 pizzas |
| WIP total final | 78 pizzas |
*Cada simulación presentará resultados diferentes
Lo más llamativo de este escenario, junto a la confirmación de que la productividad del sistema se rige por su restricción, es el efecto sistémico de la desincronización, desde la simplicidad: ¡El desbalance del flujo! (No confundir con el balance de capacidad). El efecto salta a la vista: ¡Exceso de inventario en proceso! ¡Costo de capital! ¡Caos!
Piense por un segundo, ¿Qué pasaría si subordinamos el sistema a la restricción? Creo que la pregunta debe ser otra: ¿Qué es subordinar el sistema a la restricción? En este caso, balancear el flujo subordinado a la capacidad real de la restricción. Pensemos en el efecto de establecer una política que no permita que la estación B envía hacia C (la restricción), unidades que sobrepasen un WIP determinado. El efecto sería lógico, el exceso de WIP se trasladaría hacia B. Por lo tanto, pensemos en subirdinar las estaciones previas: WIP de B y WIP de C (lo cual limitaría el procesamiento, no la capacidad), veamos esto en el siguiente escenario.
Juego 6: ¡Subordine sus sistema a la restricción! ¡NO a las eficiencias locales!
Empecemos este escenario donde finalizamos el anterior. Vamos a subordinar el sistema a la restricción (estación C), por medio de una decisión, no se procesan pizzas en las estaciones previas, por encima de un cierto nivel de inventario. Para este caso, vamos a establecer ese WIP máximo como 6:

Veamos el resultado de una simulación particular:
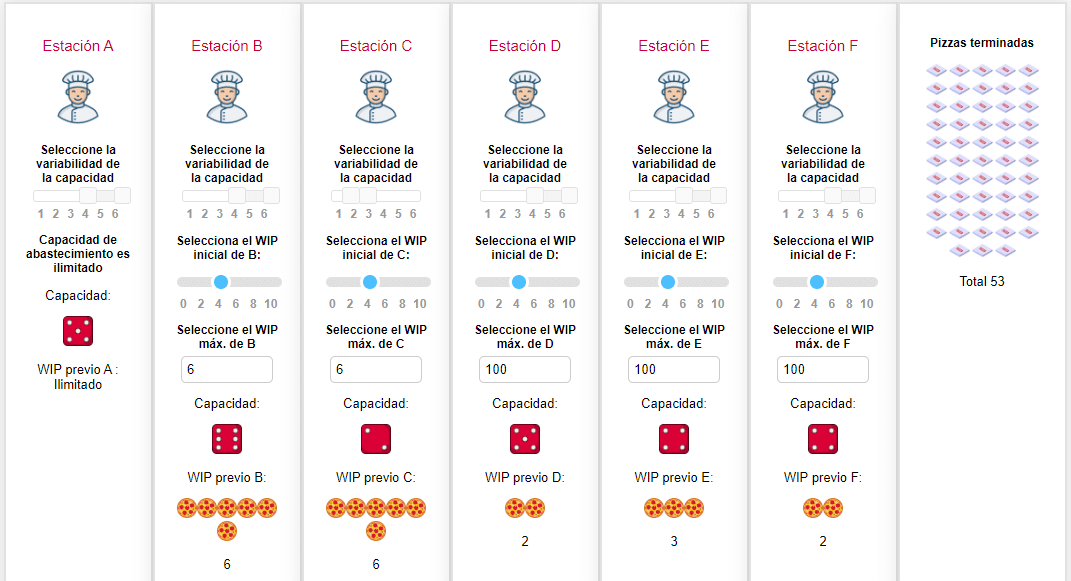
| Mínima capacidad media de las estaciones | 2,5 pizzas |
| Producción estimada de acuerdo a la estación restricción | 50 pizzas |
| Producción simulada con variabilidad (Throughput) | 53 pizzas |
| Tasa producción real / estimada por capacidad mínima | 106,00 %* |
| WIP total inicial | 20 pizzas |
| WIP total final | 19 pizzas |
*La producción real está por encima de la capacidad estimada debido al Throghput de las primeras rondas que estaba determinado por el WIP inicial de 4 pizzas (por encima de las 2,5 pizzas de la capacidad media de la restricción).
En este caso, los resultados son evidentes, subordinar el sistema, mediante una decisión que sincroniza el flujo de las estaciones que preceden a la restricción, disminuye la presión que se ejerce y se materializa en el WIP previo a la estación C. La disminución de WIP total del sistema al finalizar la simulación fue clara, pasando de 78 pizzas en proceso a 19 pizzas en proceso, y conservando la producción de pizzas terminadas del sistema. En un contexto práctico, estaríamos hablando de una disminución del capital invertido (inventario), a través de disminuir las eficiencias locales. El objetivo de la gestión de las operaciones, del Ingeniero Industrial, no pasa por hacer todas las operaciones eficientes, eso es un paradigma (muchas veces impulsado por la academia).
Veamos cómo decidimos sobre la eficiencia de B (disminuyendo su eficiencia: producción siempre por debajo de su capacidad):
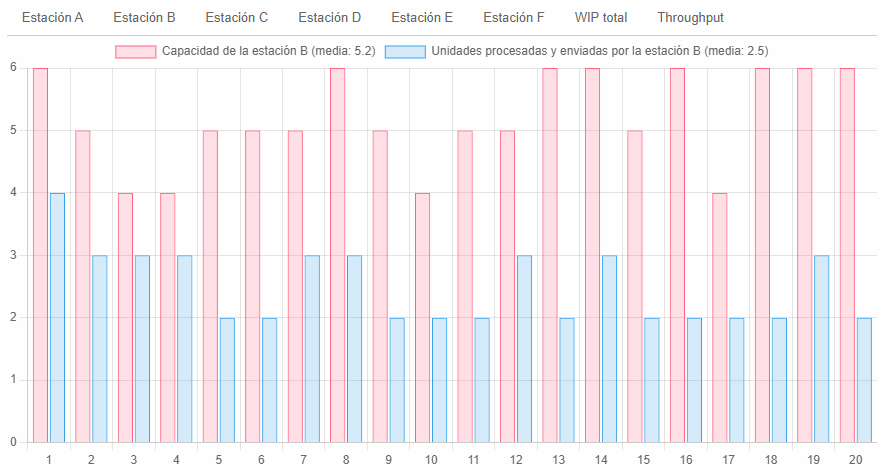
Y de ninguna manera, afectamos negativamente la productividad del sistema, por cuanto la restricción siempre estuvo protegida mediante un WIP conservador:
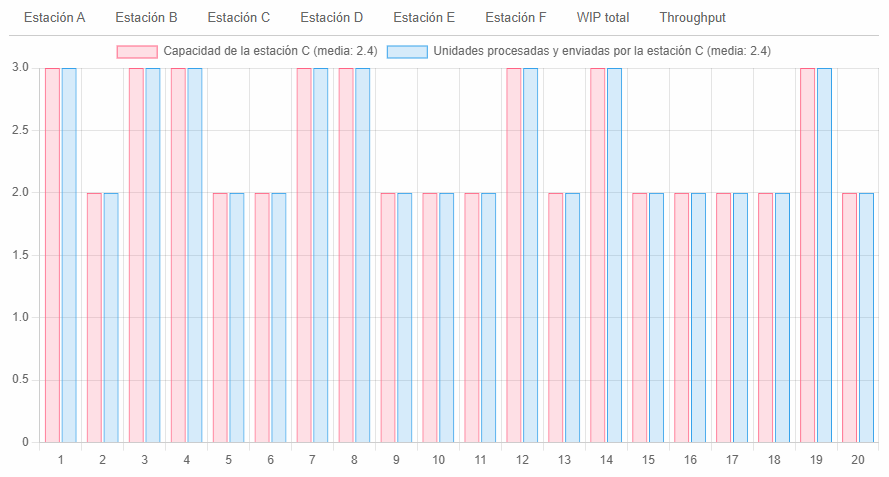
En la imagen podemos observar como en la restricción la eficiencia (protegida por el WIP) fue del 100%.
«Una hora perdida en la restrición es una hora perdida en todo el sistema. Una hora ganada donde no hay una resricción es un espejismo». Eliyahu Goldratt
